Area of Trapezium? Easy, or is it?
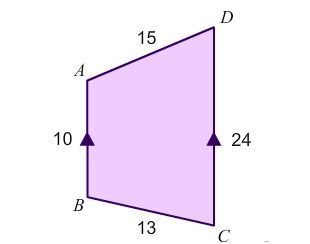 A
B
C
D
is a quadrilateral with measurements of its sides shown in the above diagram. If
A
B
is parallel to
C
D
. What is the area of the quadrilateral?
A
B
C
D
is a quadrilateral with measurements of its sides shown in the above diagram. If
A
B
is parallel to
C
D
. What is the area of the quadrilateral?
The answer is 204.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
The most important thing is to know the height of the trapezoid, which is 9. Then the rest is ice cream! Just substitute the values on the formula of the trapezoid to get the answer 2 0 4 .
Drop perpendiculars from B and A to intersect C D at E and F , respectively. Let C D = a , F D = b , and B E = h . Since B A = E F = 1 0 , so 2 4 = C D = C E + E F + F D = a + 1 0 + b , ( 1 ) a + b = 1 4 . By Pythagorean theorem and using (1), we have B C 2 − C E 2 = B E 2 = A F 2 = A D 2 − F D 2 , 1 3 2 − a 2 = h 2 = 1 5 2 − b 2 , b 2 − a 2 = 1 5 2 − 1 3 2 , ( b − a ) ( a + b ) = ( 1 5 − 1 3 ) ( 1 5 + 1 3 ) 1 4 ( b − a ) = 5 6 , ( 2 ) b − a = 4 . Adding and subtracting (1) and (2), we have 2 b = 1 8 and 2 a = 1 0 , or b = 9 and a = 5 . Thus B C 2 − C E 2 = B E 2 , 1 3 2 − a 2 = h 2 , h = 1 2 . And it follows that the area of the trapezoid is 2 ( A B + C D ) × B E = 2 ( 1 0 + 2 4 ) × 1 2 = 2 0 4 .
Drop altitudes from B to E and A to F, both on CD. Length is h.
This creates two right triangles, BCE and ADF.
Let CE = x and DF = y
13^2 = x^2 + h^2 and 15^2 = y^2 + h^2 and x + y = 14 ===> y = 14 - x
Substituting for y and solving each equation for h^2 we get:
169 - x^2 = 225 - x^2 + 28x - 196
Solving: 140 = 28x =====> x = 5
5^2 + h^2 = 13^2 = 169
h^2 = 144 ====> h = 12
Area = 0.5 (b1 +b2) h = .5 (10+24) 12 = 204 in^2
Yeah, I knew you could solve simultaneous triangles, but I couldn't figure out any shorter way to do it.
Since the quadrilateral is a trapezoid, the area is equal to (a+b)/2 times h, where a and b are the parallel sides and h the distance between them. To find the value of h, one can use the formula h=sqr((-a+b+c+d)(a-b+c+d) (a-b+c-d) (a-b-c+d))/2 times abs(b-a). In this case it reduces to sqr((42) times (14) times (-16) times (-12))/28 or 336/28 which equals 12. Multiply by (24+10)/2 or 17, and you get the answer of 204.
The figure is a trapezoid with area = (h/2)(10 + 24), where h is the height equal to the perpendiculars drawn from B to CD and A to CD.. If the perpendicular from B meets CD at point P, let PC = x. Then at the other end of CD if the perpendicular from A meets CD at Q, QD = 14 -x. Using the Pythagorean theorem twice, we have the equations: x^2 + h^2 = 169 and h^2 + (14 - x)^2 = 225. These are easily solved for x = 5, h= 12, and the area = (12/2)(10 + 24) = 204. Ed Gray
Divide the trapezium into 2 triangles by drawing the line segment BD, call this distance x. By alternating angles, angle ABD = angle BDC. Call these angles theta. Apply the cosine rule to the triangles ABD and BDC creating simultaneous equations in terms of x and theta. These solve to give x = root 505 and cos theta = 19/root505. Use sin^2+cos^2=1 to obtain sin theta. Apply 1/2 abSinC to each triangle and sum to give required result.