Partitioning triangles
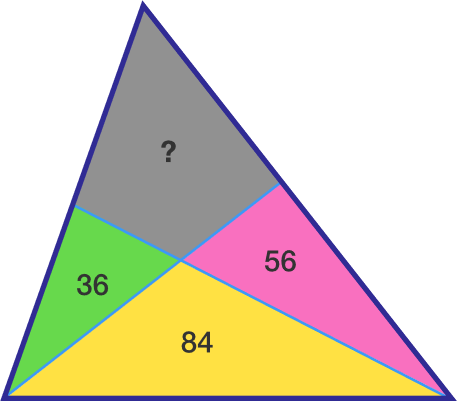
The triangle above is divided into 4 regions. The areas of the 3 triangles are given.
What is the area of the shaded region?
The answer is 104.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
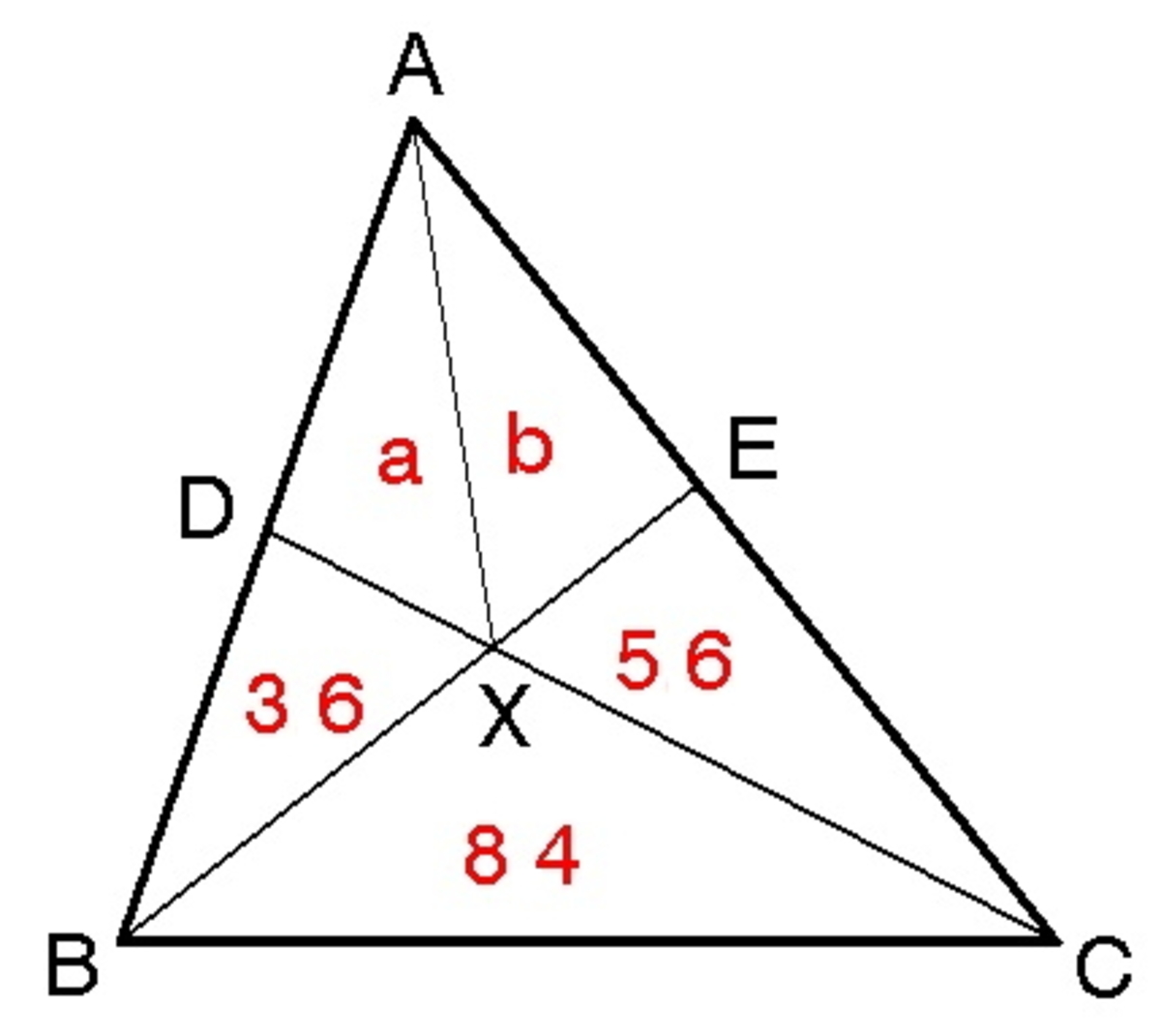
Let X be the point of intersection of lines inside the triangle. Divide the area of the shaded region into 2 parts. Name them as a and b . Observed that triangle A X D and triangle B X D share the same altitude from X , so the ratio of their areas is the same as the ratio of their bases. Similarly, triangle A C D and triangle B C D share the same altitude from C , so the ratio of their areas is the same as the ratio of their bases. Moreover, the bases are the same, and thus in the same ratio. As a result, we have:
3 6 a = 3 6 + 8 4 a + b + 5 6
After simplfying the above equation we get
a = 7 3 b + 2 4 ( 1 )
Applying the same principle to the triangles with the bases E A and E C , we have
5 6 b = 5 6 + 8 4 a + b + 3 6
After simplifying the equation above, we get
8 4 b = 5 6 a + 2 0 1 . 6 ( 2 )
Substituting ( 1 ) to ( 2 ) , we get
b = 5 6
It follows that
a = 4 8
Finally, the area of the shaded region is 5 6 + 4 8 = 1 0 4
It is worth noting that this argument can be generalised to give an elegant result.
Using Marvin's ideas, we have x a = x + y a + b + z z b = y + z a + b + x and hence a y − b x = x z − a z + b y = x z and hence a = y 2 − x z x z ( x + y ) b = y 2 − x z x z ( y + z ) If Δ is the area of the whole triangle, then Δ = a + b + x + y + z = y 2 − x z y ( x + y ) ( y + z ) and hence Δ 1 + y 1 = y ( x + y ) ( y + z ) y 2 − x z + y 1 = ( x + y ) ( y + z ) x + 2 y + z so that Δ 1 + y 1 = x + y 1 + y + z 1 a result sometimes called the Ladder Theorem. In this case, therefore, Δ 1 + 8 4 1 = 1 2 0 1 + 1 4 0 1 so that Δ = 2 8 0 , which makes the shaded area 2 8 0 − 3 6 − 8 4 − 5 6 = 1 0 4 .