Intersecting Triangles
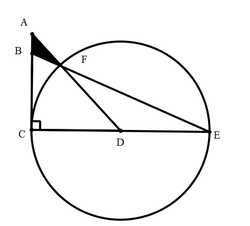 Diagram above shows a circle with center
D
, with
C
,
E
,
F
be points lying on the circle, and two right triangles
A
C
D
and
B
C
E
with their hypotenuse intersect at
F
. If we are given
A
C
=
C
D
=
1
0
cm
. What is the area of triangle
A
B
F
to 4 decimal places.
Diagram above shows a circle with center
D
, with
C
,
E
,
F
be points lying on the circle, and two right triangles
A
C
D
and
B
C
E
with their hypotenuse intersect at
F
. If we are given
A
C
=
C
D
=
1
0
cm
. What is the area of triangle
A
B
F
to 4 decimal places.
Details and Assumptions
- You may use the approximation: 2 = 1 . 4 1 4 2 1 3 5 6
The answer is 2.5126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Visually we see that the areas of the triangles are related as follows Δ A B F = Δ A C D − Δ E B C + Δ D F E
The area of ACD is: Δ A C D = 2 ∣ A C ∣ ∣ C D ∣ = 2 1 0 2 = 5 0
For the area of D F E we need it's height h F which we can calculate from Pythagoras' theorem:
h F 2 + h F 2 = ∣ D F ∣ 2 ⟹ h F = 5 0 Therefore: Δ D F E = 2 h F ∣ D E ∣ = 2 1 0 h F = 5 5 0
For the area of E B C we need it's height ∣ B C ∣ . If we denote by F x the point between C D that makes D F F x a right-angled triangle, then we see that since E F F x and C B E are congruent it must be the case that
∣ C E ∣ ∣ B C ∣ = ∣ F x E ∣ ∣ F F x ∣ = h F + ∣ D E ∣ h F ⟹ ∣ B C ∣ = 1 0 + h F 2 0 h F = 1 0 + 5 0 2 0 5 0 Therefore: Δ C B E = 2 ∣ B C ∣ ∣ C E ∣ = 1 0 ∣ B C ∣ = 1 0 + 5 0 2 0 0 5 0
Substituting the initial equation, we get:
Δ A B F = 5 0 − 1 0 + 5 0 2 0 0 5 0 + 5 5 0 ≈ 2 . 5 1 3
Can You PLease explain how you got the height of Tr. DEF??
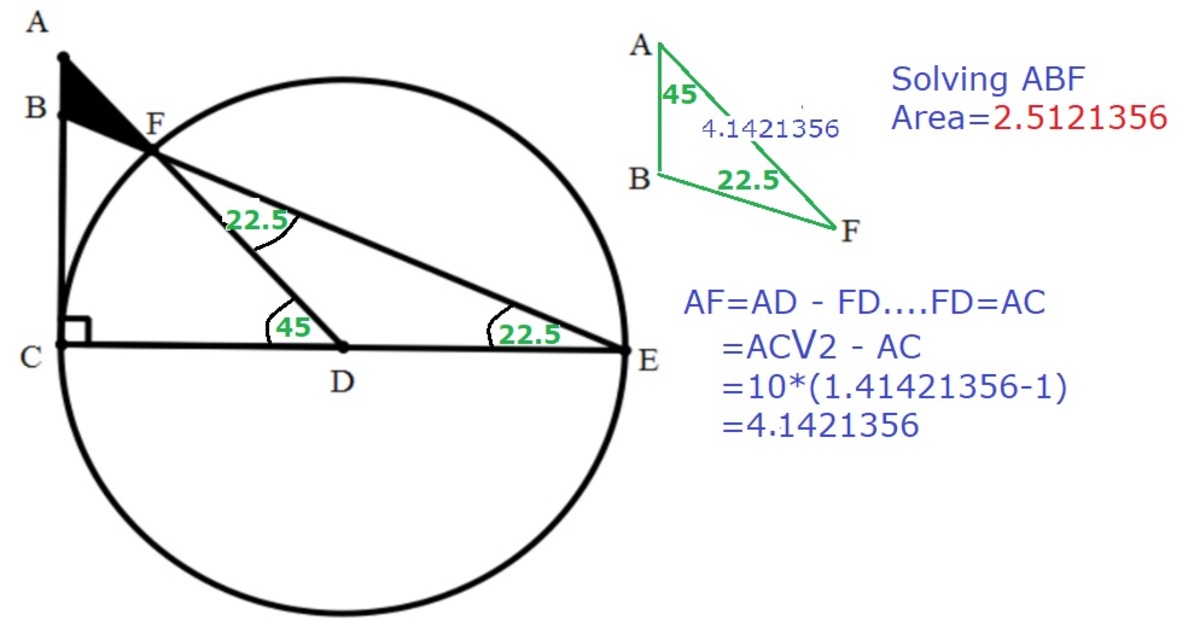
Area ABF = Area ACD + Area FDE - AreaBCE
= (10 * 10)/2 + (10 sin 45 * 10)/2 - ( 20 tan 22.5* 20)/2
= 50 + 35.355339 - 82.842712
= 2.51262
= 2.5126