Area: Pentagon with a circular hole
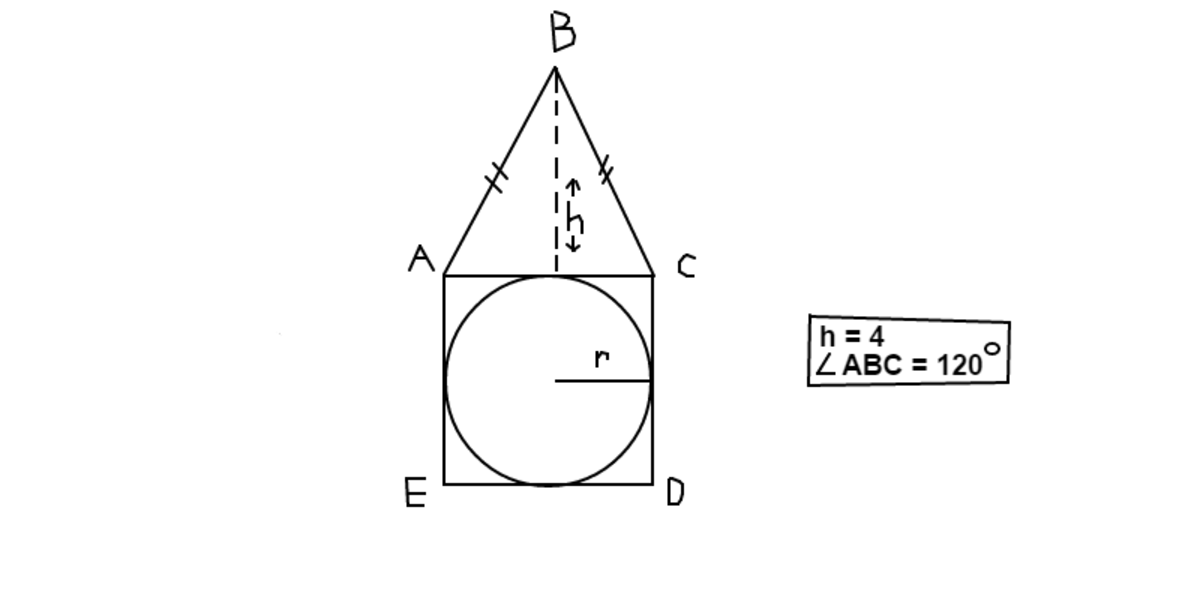
The image above consists of an isosceles triangle, △ A B C where the height: h = 4 units ; A B = B C ; and ∠ A B C = 1 2 0 ∘ . △ A B C lies on top of the square A C D E and a circle of radius r is inscribed in the square A C D E . Determine the area of the pentagon formed from combining the triangle A B C and the square A C D E minus the area of the inscribed circle.
Give your answer to one decimal place.
The answer is 68.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Δ A C B i s 3 0 − 3 0 − 1 2 0 . ∴ A C = 2 ∗ h ∗ C o t 3 0 = 2 ∗ 4 ∗ 3 . = 8 3 . A r e a s P e n t a g o n − c i r c l e = a r e a s Δ A C B + □ A E D C − c i r c l e , A r e a s P e n t a g o n − c i r c l e = 2 1 ∗ 8 3 ∗ 4 + ( 8 3 ) 2 − π ∗ 4 8 3 ) 2 A r e a s P e n t a g o n − c i r c l e = 1 6 3 + 1 9 2 − 4 8 ∗ π = 6 8 . 9 .
△ A B C can be split into two congruent right triangles with legs h and r and an angle of 6 0 ∘ . To determine r : t a n ( 6 0 ∘ ) = r / 4 ⇒ r = 4 t a n ( 6 0 ∘ ) = 4 3 u n i t s The areas of each shape can be calculated as follows: A r e a o f △ A B C = 2 1 × h × 2 r = 2 4 ( 8 3 ) = 1 6 3 u n i t s 2 A r e a o f □ A C D E = ( 2 r ) 2 = ( 8 3 ) 2 = 6 4 ( 3 ) = 1 9 2 u n i t s 2 A r e a o f ◯ = π r 2 = π ( 4 3 ) 2 = 4 8 π u n i t s 2
A n s w e r : 1 9 2 + 1 6 3 − 4 8 π ≈ 6 8 . 9 u n i t s 2