Area Problem 3
Geometry
Level
4
In the diagram,
- the centers of the two circles are at the midpoints of adjacent sides of a regular pentagon;
- the two circles intersect at the center of the pentagon;
- the area of the pentagon is 900.
What is the total area of the red regions?
The answer is 540.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
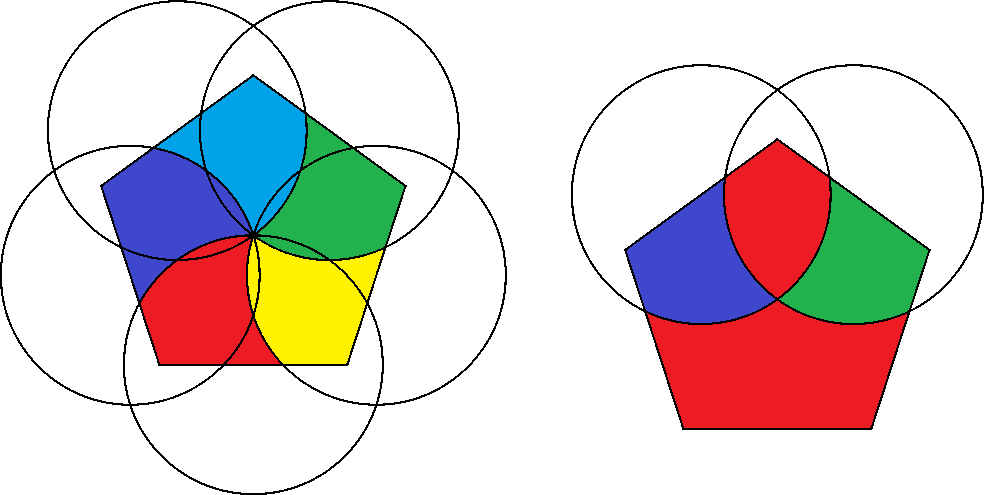
Therefore the area of the red region is 5 3 the area of the pentagon or A r e d = 5 3 A p e n t a g o n = 5 3 × 9 0 0 = 5 4 0 .