Area Properties Of Triangles
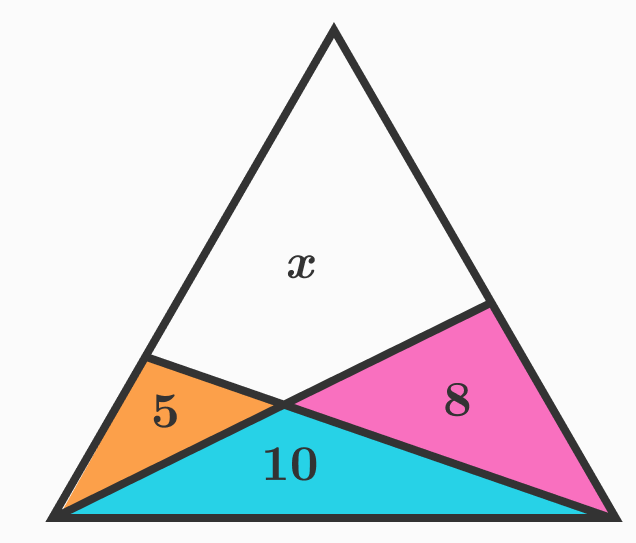
In the above triangle which is divided into four regions, the numbers each refer to the area of the corresponding region.
What is the value of x ?
Note: Image not necessarily drawn up to scale.
This is a shared problem from A. Gardiner's, An introduction to problem solving handbook. The triangle is not necessarily equilateral or isosceles.
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Nice solution using just that simple idea of area ratios.
How do we know that XD XE are perpendicular to the repsective sides AB AC?
Log in to reply
They need not be perpendicular. We are taking the "height of X to base AB", "height of C to base AB", etc.
I think you made a little mistake. It will be b=2*10-8=12.. But you have write the right answer ;)
A complete discussion of the solution to this problem, including proofs of the theorems used, can be found here .
I don't know if the author of this work invented the names "Crossed Ladder Theorem" and "Extended Crossed Ladder Theorem" but it looks like Menelaus's Theorem is embedded in there !!
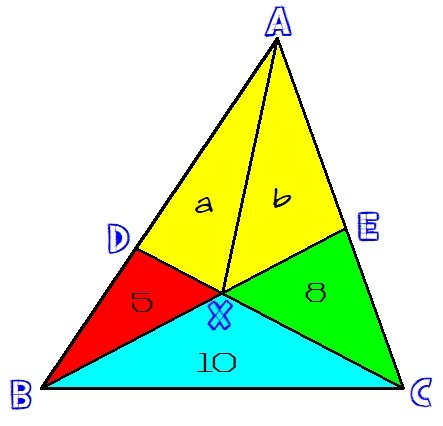 Consider the diagram. Recall that the areas of triangles with equal altitudes are proportional to the bases of the triangles. We have,
Consider the diagram. Recall that the areas of triangles with equal altitudes are proportional to the bases of the triangles. We have,
D B A D = A C D B A C D A = A X D B A X D A
5 + 1 0 a + b + 8 = 5 a ⟹ 5 ( a + b + 8 ) = 1 5 a ⟹ a + b + 8 = 3 a ⟹ b + 8 = 2 a ( 1 )
E C A E = A B E C A A B E = A E X C A A X E
8 + 1 0 a + b + 5 = 8 b ⟹ 8 ( a + b + 5 ) = 1 8 b ⟹ 4 a + 4 b + 2 0 = 9 b ⟹ 4 a + 2 0 = 5 b ( 2 )
Substitute ( 1 ) in ( 2 ) , we have
2 ( b + 8 ) + 2 0 = 5 b ⟹ 2 b + 1 6 + 2 0 = 5 b ⟹ 3 6 = 3 b ⟹ 1 2 = b
It follows that,
2 a = b + 8 = 1 2 + 8 = 2 0 ⟹ a = 1 0
Finally, the area of the yellow region is a + b = 1 0 + 1 2 = 2 2
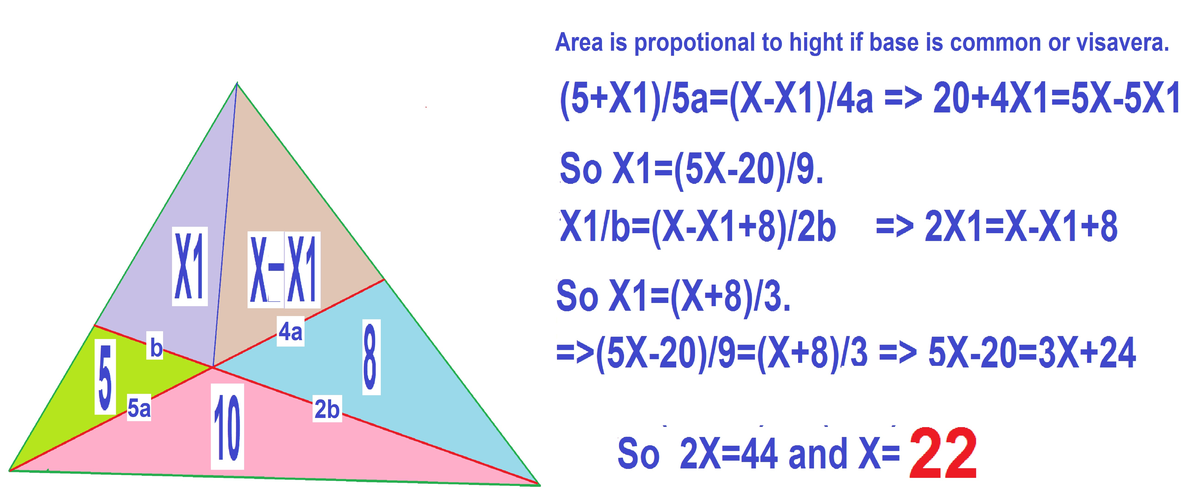
Please refer to Patryk's diagram. Tr. DXE = 4 unit² because Tr.DBX / Tr.CBX = 5/10 = 1/2. Now apply Menelaus's Theorem to Tr. ADC with BXE as the transversal to get: (12/(x-4)) ((x+5)/9) (1/2)=1 which yields x = 22 unit²
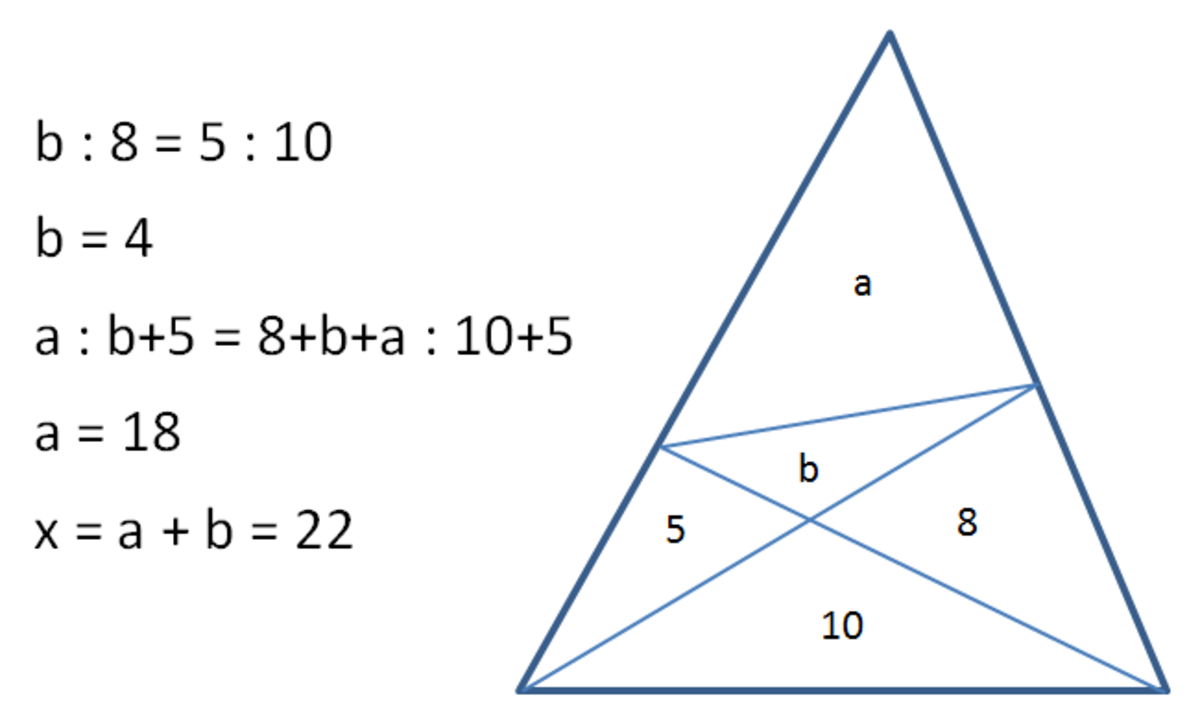
Let's split area x from the vertex, such that x = a + b .
We will use the fact that for triangles with the same height (or base), the ratio of their areas is the ratio of their base (or height).
Triangles A X D and B X D along base A B have identical heights. Therefore, their areas must in the ratio of their bases:
a : 5 = A D : D B
Triangles A C D and B C D along base A B have identical heights. Therefore, their areas must be in the ratio of their bases:
a + b + 8 : 5 + 1 0 = A D : D B
Since these 2 sets of triangles have the same base, we conclude that
a : 5 = A D : D B = ( a + b + 8 ) : 1 5 ⇒ b = 2 a − 8
We repeat this process on the other side.
Triangles A X E and C X E along base A C have identical heights. Therefore, their areas must be in the ratio of their bases:
b : 8 = A E : E C
Triangles A B E and C B E along base A C have identical heights. Therefore, their areas must be in the ratio of their bases:
a + b + 5 : 8 + 1 0 = A E : E C
Since these 2 sets of triangles have the same base, we conclude that
b : 8 = A E : E C = ( a + b + 5 ) : 1 8 ⇒ 5 b = 4 a + 2 0
Solving these 2 equations, we obtain 5 ( 2 b − 8 ) = 4 a + 2 0 ⇒ a = 1 0 , b = 2 × 1 0 − 8 = 1 2 .
Hence, x = a + b = 1 0 + 1 2 = 2 2