Area ratio of two circles?
The problem's question is: "What is the ratio of the area of the larger circle divided by the area of the smaller circle?"
Select a random triangle on the Euclidean plane. The triangle must have a positive area. It may be acute or obtuse, but, not right. Compute the circumsphere or circumscribed sphere (meaning the same kind of entity) of the triangle's vertices. Drop perpendiculars from each vertex onto the extended, if necessary, opposite side of the triangle. These perpendiculars are sometimes called altitudes. The point of intersection of the altitudes with the opposite sides I am calling the feet of the altitudes. Compute another circumsphere that goes through the feet. One of these two circumspheres is smaller than the other. Divide the smaller circumsphere's area into the larger circumsphere's area. The ratio is the answer.
Note: the answer will not have a factor of in it and it will be a algebraic number.
Note. neither coordinates of the original triangle's vertices nor the lengths of the triangle's sides are provided. The answer is not dependent on these data.
Here is an unlabeled diagram:
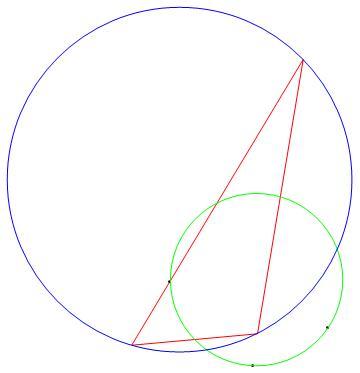
The answer is 4.0000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
See 9-point circle : The radius of a triangle's circumcircle is twice the radius of that triangle's nine-point circle.
The procedure described in the problem is one way of computing a triangle's 9-point circle.