Area Ratio of Two Triangles

Each cevian in △ A B C partitions its opposite side in a 2 : 3 ratio: D B A D = E C B E = F A C F = 3 2 . If the area ratio of △ A B C to △ I J K is q p , what is p + q ?
The figure is not drawn to scale.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Good job! That's what I was hoping for.
Log in to reply
Thanks for your problem. I learn about Routh's theorem now.
awesome sum man.
Since we are interested in the ratio of areas, it suffices to consider a particular triangle △ A B C , whose vertices are A ( 0 , 0 ) , B ( 5 , 1 0 ) , C ( 1 5 , 0 ) . Then the position coordinates of D , E , F are ( 2 , 4 ) , ( 9 , 6 ) , ( 9 , 0 ) respectively. Equations of A E , B F , C D are y = 3 2 x , y = 2 5 ( 9 − x ) , y = 1 3 4 ( 1 5 − x ) respectively. Hence the position coordinates of I , J , K are ( 1 9 1 3 5 , 1 9 9 0 ) , ( 1 9 9 0 , 1 9 6 0 ) , ( 1 9 1 5 5 , 1 9 4 0 ) respectively. Hence, area of △ A B C is 2 1 × 1 5 × 1 0 = 7 5 , and of △ I J K is 2 1 ∣ 1 9 1 3 5 ( 1 9 6 0 − 1 9 4 0 ) + 1 9 9 0 ( 1 9 4 0 − 1 9 9 0 ) + 1 9 1 5 5 ( 1 9 9 0 − 1 9 6 0 ) ∣ = 1 9 7 5 , and the required ratio is 1 9 1 . Hence p = 1 , q = 1 9 and p + q = 1 + 1 9 = 2 0 .
It is always true because every triangle can be converted to any other triangle using linear transformation, and it doesn't change the ratio of areas.
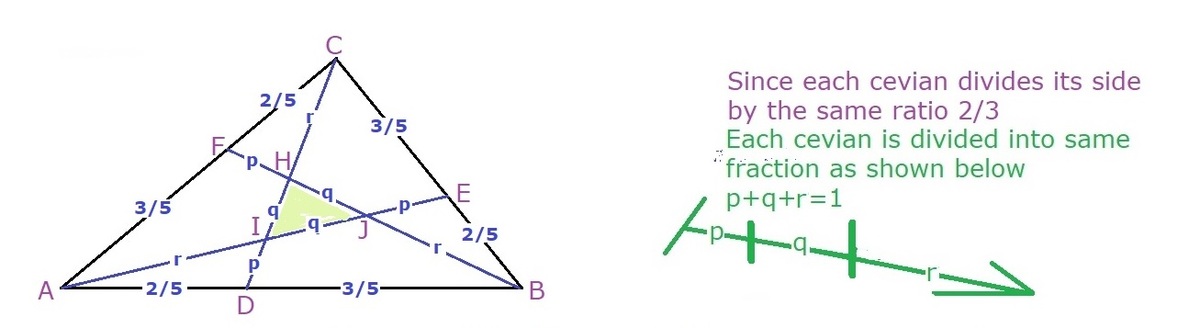
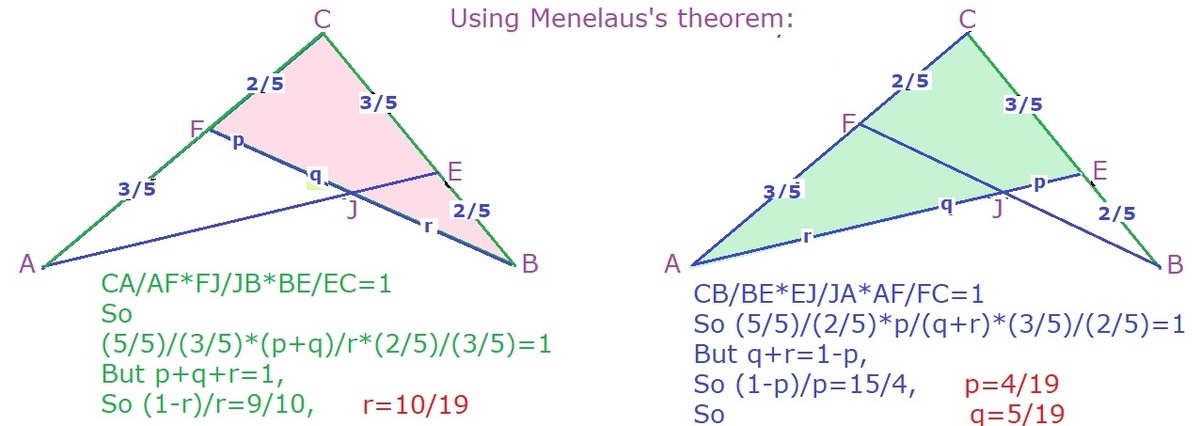
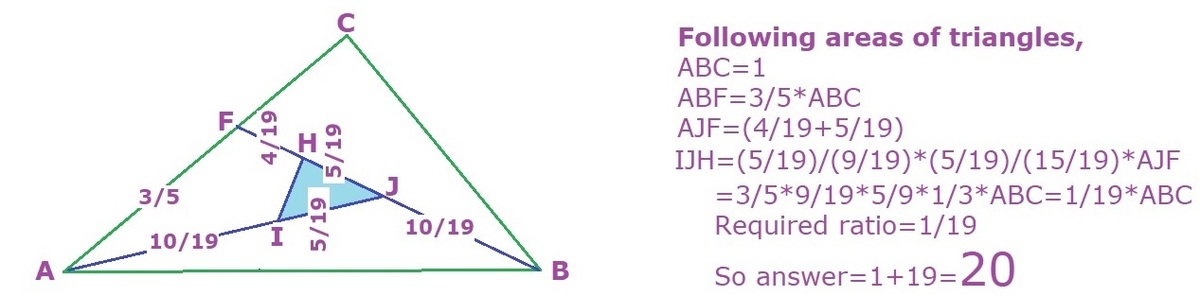
We neglect the -tive sign in the equation.
If each cevian divide its side in the same ratio, the triangle formed in side is an equivalent.
Skewing △ A B C to an equilateral triangle will preserve the ratio of areas, so let a = A D = B E = C F and b = A F = B D = C E . Also let c = A E = B F = C D .
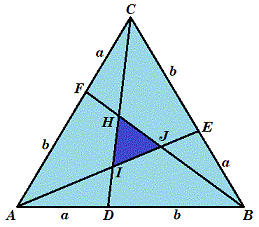
△ A B E ∼ △ A I D by AA similarity, so A B A I = A E A D or a + b A I = c a or A I = c a ( a + b ) , and B E I D = A E A D or a I D = c a or I D = c a 2 .
Now A E = A I + I J + J E , so c = c a ( a + b ) + I J + c a 2 , which solves to I J = c c 2 − a b − 2 a 2 .
The ratio of sides between △ A B C and △ I J K is A B I J = c ( a + b ) c 2 − a b − 2 a 2 , so the ratio of areas is r = c 2 ( a + b ) 2 ( c 2 − a b − 2 a 2 ) 2 .
By the law of cosines on △ A C D , c 2 = a 2 + ( a + b ) 2 − 2 a ( a + b ) cos 6 0 ° , or c 2 = a 2 + a b + b 2 .
Substituting c 2 = a 2 + a b + b 2 into the ratio of areas r = c 2 ( a + b ) 2 ( c 2 − a b − 2 a 2 ) 2 and simplifying gives:
r = a 2 + a b + b 2 ( b − a ) 2 .
In this question, a = 2 and b = 3 , so the area ratio of △ A B C and △ I J K is r = a 2 + a b + b 2 ( b − a ) 2 = 2 2 + 2 ⋅ 3 + 3 2 ( 3 − 2 ) 2 = 1 9 1 , which means p = 1 , q = 1 9 , and p + q = 2 0 .
Very clever. I like!
By Routh's theorem , if (as shown in the figure of the problem) D B A D = x , E C B E = y , and F A C F = z . Then the area of △ I J K is given by:
[ I J K ] ⟹ [ A B C ] [ I J K ] = ( x y + y − 1 ) ( y z + z + 1 ) ( z x + x + 1 ) ( x y z + 1 ) 2 [ A B C ] = ( ( 3 2 ) 2 + 3 2 + 1 ) 3 ( ( 3 2 ) 3 − 1 ) 2 = ( 9 1 9 ) 3 ( − 2 7 1 9 ) 2 = 1 9 1
Therefore, p + q = 1 + 1 9 = 2 0 .