Area to volume
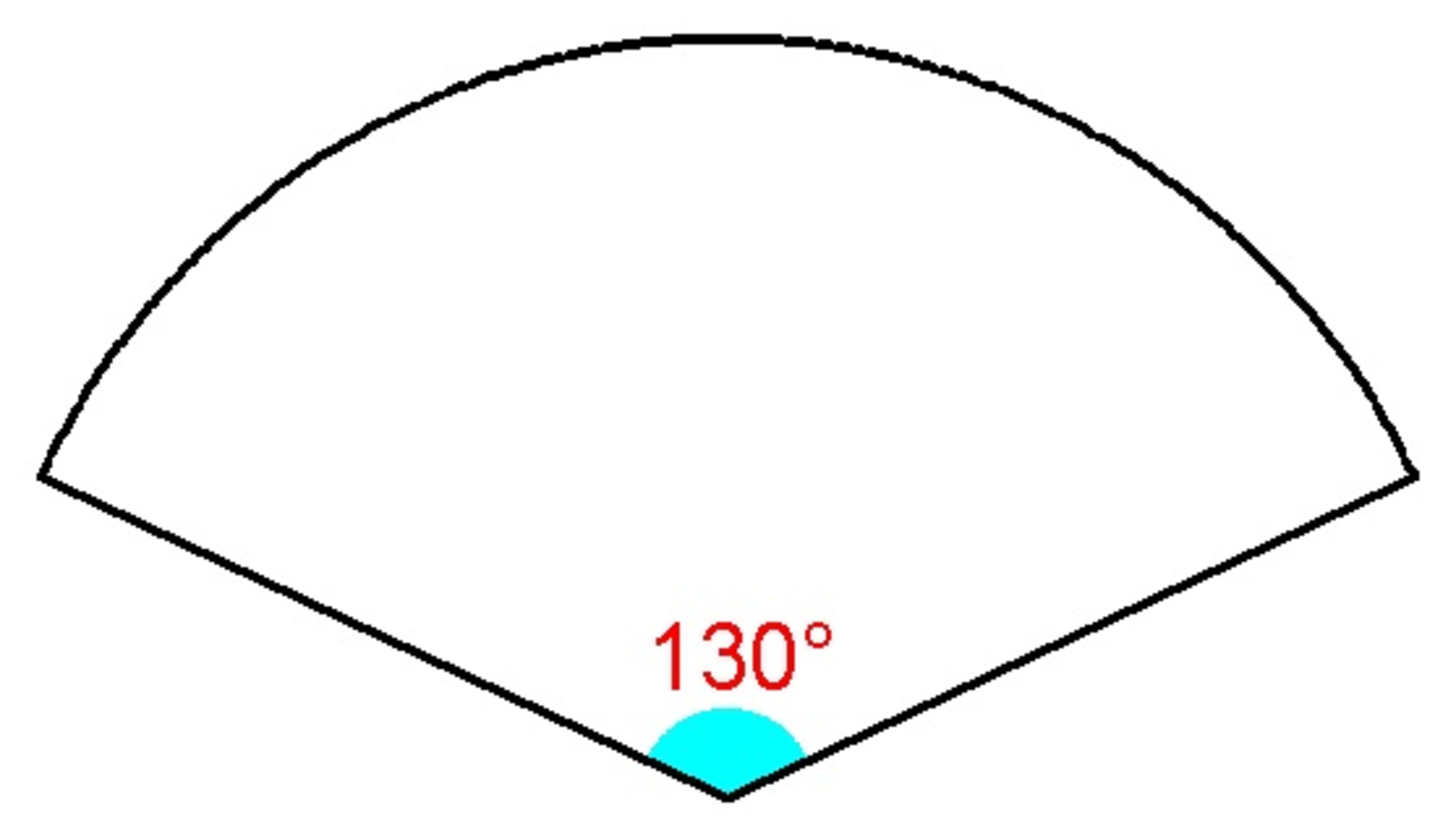 The area of the sector shown above is
. It is to be rolled to form a right circular cone. Find the volume of the cone. If your answer can be expressed as
, where
and
are coprime positive integers, give your answer as
.
The area of the sector shown above is
. It is to be rolled to form a right circular cone. Find the volume of the cone. If your answer can be expressed as
, where
and
are coprime positive integers, give your answer as
.
The answer is 150062.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Considering the sector of the circle:
let L be the radius of the sector of the circle and c be the arc length. Then
9 1 3 0 0 π = 3 6 0 1 3 0 π ( L 2 ) ⟹ L = 2 0
c = 3 6 0 1 3 0 ( 2 ) ( π ) ( 2 0 ) = 9 1 3 0 π
Considering the right circular cone:
The arc length of the sector is equal to the circumference of the base of the cone , so we have 9 1 3 0 π = 2 π r ⟹ r = 9 6 5
By the pythagorean theorem , we have h = 2 0 2 − ( 9 6 5 ) 2 = 8 1 2 8 1 7 5 = 9 3 5 2 3
Hence, the volume of the cone is,
V = 3 1 π r 2 h = 3 1 π ( 9 6 5 ) 2 ( 9 3 5 2 3 ) = 2 1 8 7 1 4 7 8 7 5 π 2 3
Finally,
a + b = 1 4 7 8 7 5 + 2 1 8 7 = 1 5 0 0 6 2