Area under envelope of a family of lines
For 0 ≤ t ≤ 1 we define a family of lines connecting the two points ( t , 0 ) and ( 0 , 1 − t ) . This family of lines defines an envelope that is tangent to the lines where they meet. Find the equation of the envelope curve (shown in red), then find the area bounded by the curve, the x axis and the y axis. If this area can be written as q p for positive coprime integers p , q , find p + q
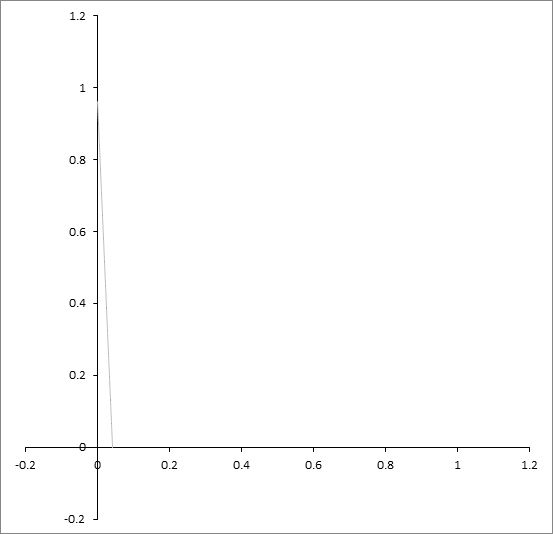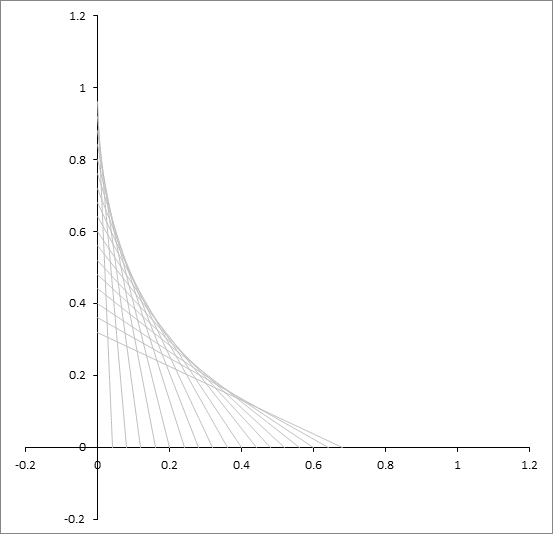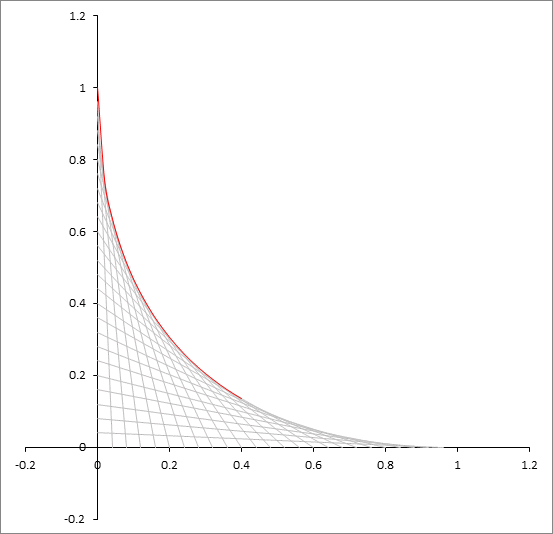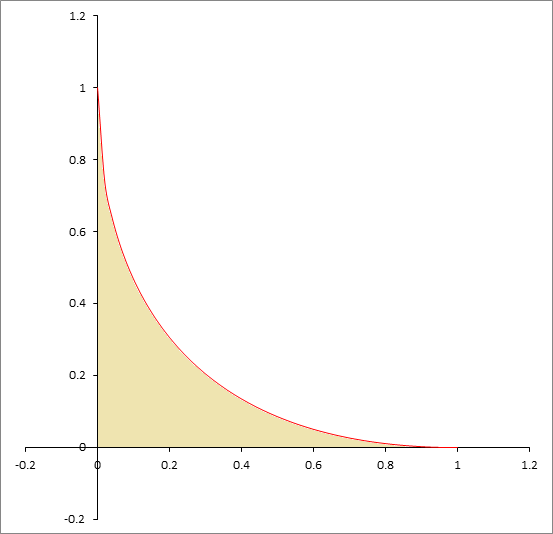
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The straight line from ( t , 0 ) to ( 0 , 1 − t ) has equation ( 1 − t ) x + t y = t ( 1 − t ) We obtain the envelope by differentiating this partially with respect to t , so y − x = 1 − 2 t and eliminating t from these two equations. This yields 2 ( x + y ) = 1 + ( x − y ) 2 Solving for y gives y = x + 1 − 2 x , and hence the desired area is 6 1 , making the answer 7 .
It is interesting to rotate the coordinates by 4 5 ∘ , using the coordinates X = 2 1 ( x − y ) and Y = 2 1 ( x + y ) , which makes the equation of the envelope 2 2 Y = 1 + 2 X 2 and hence the curve is a parabola.
Each line in the family of lines has an equation of y = t − 0 0 − ( 1 − t ) x + 1 − t or y = x − t x + 1 − t .
The envelope is made up of maximum heights of these lines at a given x -coordinate, so d t d y = t 2 x − 1 = 0 , which solves to t = ± x .
Substituting t = ± x into y = x − t x + 1 − t and simplifying gives y = x − 2 x + 1 for y < 1 .
The area under the curve is then ∫ 0 1 ( x − 2 x + 1 ) d x = 6 1 , so p = 1 , q = 6 , and p + q = 7 .