Area Without Numbers
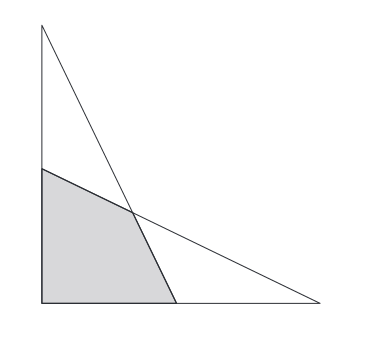
Two right triangles , both with legs measuring a and b , where a > b , are overlapping as the image above.
What is the area of the gray quadrilateral?
Source : OBMEP 2016.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice! I will study this Menelau's theorem, because it simplified the problem
the question to me was confusing at best. i thought that the question meant "a" to be the hypotenuse and "b" to be the line adjacent to the hypotenuse which is the shorter side. i hope this question gets reworded. maybe it's just me who read it differently . now im back to level 2 :(
Log in to reply
The legs of a right triangle refer to the "opposite" and "adjacent" sides, and not the "hypotenuse". It's pretty common terminology, and I think that the question is clearly phrased.
The image could be improved by displaying the lengths though.
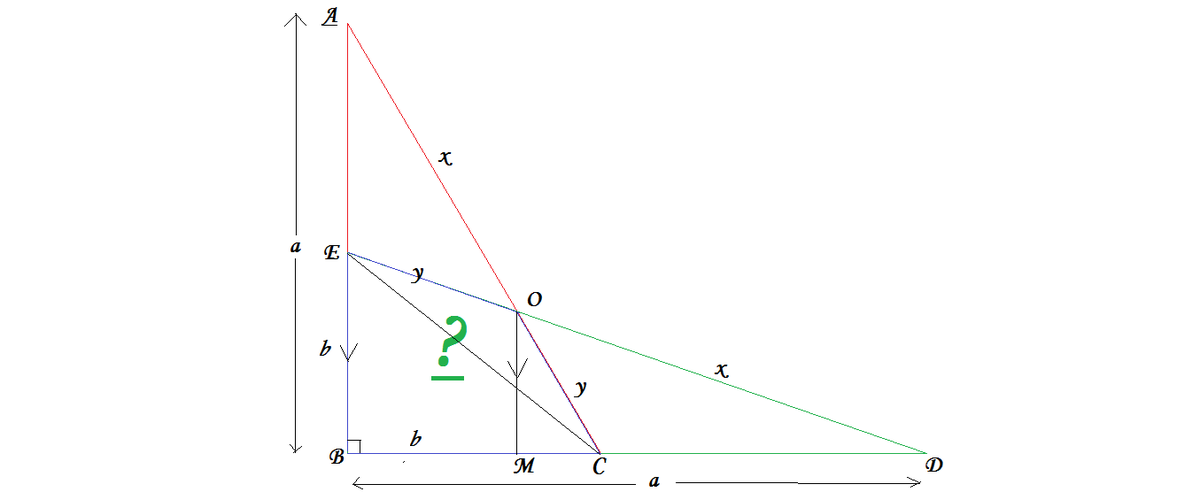
Given - ABC & BDE are two triangles which are overlapped over each other as shown in the given figure . AB = BD = a and BE = BC = b . Also, a > b . To Find - Area of quadrilateral BCOE .
Construction :- Draw OM || AB to meet BD at M. Join EC .
In the figure , let AO = DO = x and EO = CO = y .
It is clear that △ ABC ~ △ OMC
=> O M A B = O C A C
=> O M a = y x + y
=> OM = x + y a y ...................... (1)
and △ EBD ~ △ OMD
=> EB/OM = ED/OD
=> b / OM = (x+y) / x
=> OM = x + y b x ........................ (2)
From (1) and (2) x + y a y = x + y b x => ay = bx
=> x = b a y
Now , in right angled triangle ABC , AB ^2 + BC^{2} = AC^2 (By Pythagoras ' theorem ) => a ^2 + b ^2 = { x + y } ^2 => a ^2 + b ^2 = [ b a y + y ] ^2
Solving this equation we get : -
y
^2 =
(
a
+
b
)
2
(
a
2
+
b
2
)
b
2
................... (3)
Also, in right angled triangle BEC , BE^2 + BC^2 = CE^2 (By Pythagoras ' theorem ) => b ^2 + b ^2 = CE ^2 => CE = √(2b^2) ..................... ( 4 )
Now, Area of triangle COE = 1/4 * base * √{4 * ( equal sides)^2 - (base)^2} { '.' It is an isosceles triangle}
= 1/4 * EC * √{4 * y^2 - CE^2}
= 1/4 * b√2 * √{4 * ( a + b ) 2 ( a 2 + b 2 ) b 2 - (b√2)^2 }
= 2 ( a + b ) b 2 ( a − b )
Also , Area of triangle BEC = 2 1 * base * height = 2 1 BC *BE = 2 1 * b * b = 2 1 b ^2
.'. Area quadrilateral BCOE = Area of triangle COE + Area of triangle BEC
= 2 ∗ ( a + b ) b 2 ∗ ( a − b ) + 2 b 2
= 2 b 2 ∗ a − b a + b + a − b
= a − b ( a b 2 )
................................................................................................................................... By Vishwash Kumar
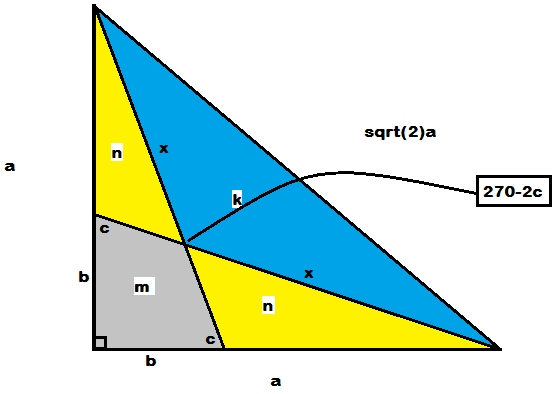
tan c = b a and from areas of regions, we have:
2 m + 2 n = a b and 2 n + m + k = 2 a 2 , from where we need the expression for m . Eliminate 2 n between the equations to get m = a b − 2 a 2 − k .
Using cosine law in region k , we have:
2 x 2 [ 1 − c o s ( 2 7 0 − 2 c ) ] = 2 a 2
⟹ x 2 [ 1 + s i n ( 2 c ) ] = a 2
⟹ x 2 [ 1 + 1 + tan 2 c 2 tan c ] = a 2
⟹ x 2 = ( a + b ) 2 a 2 ( a 2 + b 2 )
Now, area of k :
= 2 1 × x 2 × sin ( 2 7 0 − 2 c )
= 2 1 × ( a + b ) 2 a 2 ( a 2 + b 2 ) × ( − cos 2 c )
= 2 1 × ( a + b ) 2 a 2 ( a 2 + b 2 ) × b 2 a 2 + 1 b 2 a 2 − 1
= 2 1 × ( a + b ) 2 a 2 ( a 2 − b 2 )
Substituting this value of k in the above boxed equation gives us m = a + b a b 2
We proceed by cheating with coordinate geometry. Let the bottom-left corner be the origin.
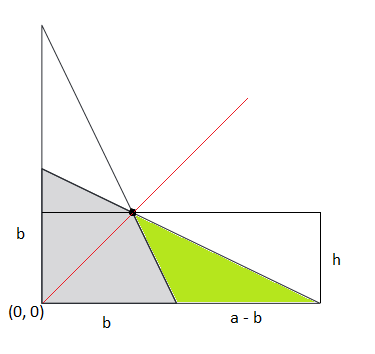
The gray area can be found by taking the area of one of the right triangles (say, the bottom one), and subtracting the area of the obtuse green triangle shown.
The area of one of the right triangles would very obviously be 2 a b .
The green triangle's length would be a − b . It's height will be the y - coordinate of the intersection of the hypotenuses of the right triangles.
Instead of finding the coordinates of the intersection by finding the equations for both of the hypotenuses, we note that the intersection lies on the line y = x , which can be shown by symmetry.
We find the equation of the hypotenuse of the bottom-most right triangle. Using slope and y - intercept, we get:
y = a − b x + b
The point in question lies on y = x , so substitute to get:
y = a − b y + b
Solve for y:
y = a b + 1 b
This is the height of the green triangle. The area would then be:
2 1 a b + 1 ( a − b ) b = 2 ( a + b ) a b ( a − b )
Recall the area of the right triangle: 2 a b
Subtract:
2 a b − 2 ( a + b ) a b ( a − b )
= 2 ( a + b ) a b ( a + b ) − 2 ( a + b ) a b ( a − b )
= 2 ( a + b ) a b ( a + b ) − a b ( a − b )
= 2 ( a + b ) a b ( a + b − a + b ) = 2 ( a + b ) a b ( 2 b ) = a + b a b 2
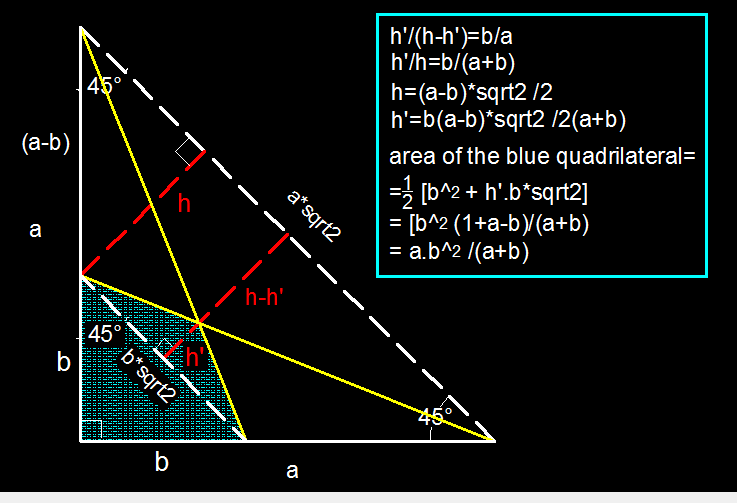
Some of the other solutions are somewhat tedious in finding the intersection point, so I'm presenting an approach using Menelaus.
By considering a base along the line AD and a height of FE, we see that
Area of A F E Area of A F G E = Area of A F E Area of A F E + Area of G F E = A H A H + H G = A H A G
We know that the area of A F E is 2 b 2 , and need to find A H A G .
Applying menelaus' theorem on triangle A D B with transversal F G E , we obtain
G D A G × E B D E × F A B F = 1 .
Thus G D A G = 1 2 × b a − b = a − b 2 b , so A D A G = a + b 2 b , so A H A G = A D A G × A H A D = a + b 2 b × b a = a + b 2 a .
Hence, Area of A F G E = 2 b 2 × a + b 2 a = a + b a b 2 .