Area Frenzy
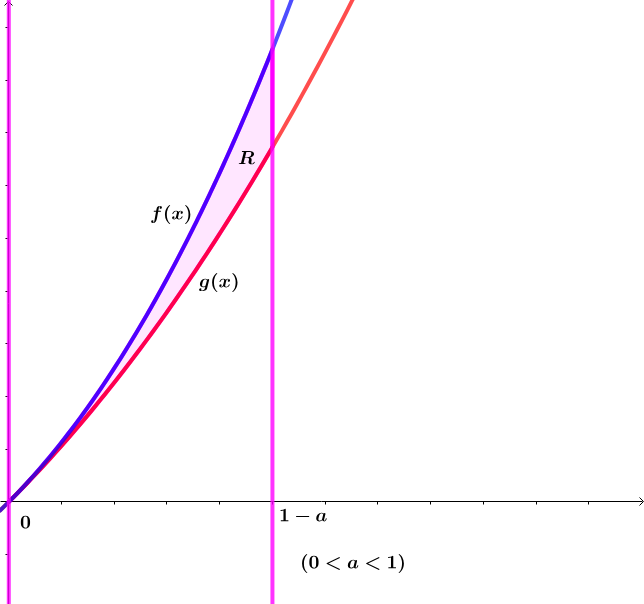
Let ∣ x ∣ < 1 and ( 0 < a < 1 ) .
If f ( x ) = ∑ n = 1 ∞ n 6 x n and g ( x ) = ∑ n = 1 ∞ n 5 x n and the region R bounded by f and g on [ 0 , 1 − a ] has area A R = a 6 1 1 a 6 − 9 4 a 5 − 9 6 0 9 a 4 + 3 1 7 0 a 3 + 3 3 0 a 2 − 4 8 8 a + 1 1 9 − 2 ln ( a ) , find the real value of a and express the answer as the value of A R to six decimal places.
The answer is 75708175.605170.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
If you want the final equation to simplify to a 6 1 0 0 0 0 a 4 − 4 0 0 0 a 3 + 6 0 0 a 2 − 4 0 a + 1 = 0 , the coefficient of a 4 in a 6 1 1 a 6 − 9 4 a 5 + 9 6 0 9 a 4 + 3 1 7 0 a 3 + 3 3 0 a 2 − 4 8 8 a + 1 1 9 − 2 lo g a should be − 9 6 0 9 .
Log in to reply
I had -9609 in my notes. It was a typing error. Thanks! I changed it. I appreciate that someone notified me. Sorry about that.
Below is a slightly altered version I posted of this problem:
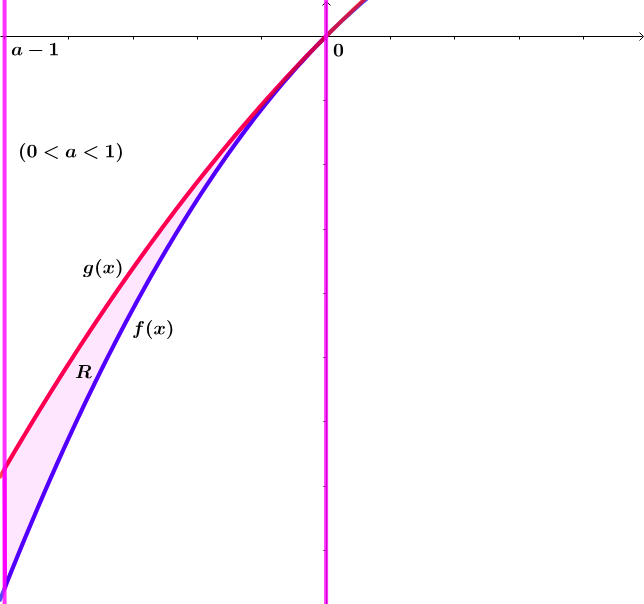
Let ∣ x ∣ < 1 and ( 0 < a < 1 ) .
If f ( x ) = ∑ n = 1 ∞ ( − 1 ) n + 1 n 6 x n and g ( x ) = ∑ n = 1 ∞ ( − 1 ) n + 1 n 5 x n and the region R bounded by f and g on [ a − 1 , 0 ] has area A R = a 6 1 1 a 6 − 9 4 a 5 − 9 6 0 9 a 4 + 3 1 7 0 a 3 + 3 3 0 a 2 − 4 8 8 a + 1 1 9 − 2 ln ( a ) , find the real value of a and express the answer as the value of A R to six decimal places.
Let ∣ x ∣ < 1 and ( 0 < a < 1 ) .
∑ n = 1 ∞ n x n = ∑ j = 1 ∞ ∑ n = j ∞ x n = 1 − x 1 ∑ j = 1 ∞ x j = 1 − x 1 ( x ) 1 − x 1 = ( 1 − x ) 2 x
( x − 1 x ) ( x 1 ) ( x − 1 x ) = ( x − 1 ) 2 x .
∑ n = 1 ∞ n 2 x n = ∑ j = 1 ∞ ( ∑ n = j ∞ n x n ) = 1 − x 1 ∑ j = 1 ∞ ( j x j ) + ( 1 − x ) 2 x ∑ j = 1 ∞ x j =
( 1 − x 1 ) ( ( 1 − x ) 2 x ) + ( ( 1 − x ) 2 x ) ( 1 − x x ) = ( 1 − x ) 3 x 2 + x .
∑ n = 1 ∞ n 3 x n = ∑ j = 1 ∞ ∑ n = j ∞ n 2 x n = 1 − x 1 ∑ j = 1 ∞ j 2 x j + ( 1 − x ) 2 2 x ∑ j = 1 ∞ j x j + ( 1 − x ) 3 x 2 + x ∑ j = 1 ∞ x j = ( 1 − x 1 ) ( ( 1 − x ) 3 x 2 + x ) + ( ( 1 − x ) 2 2 x ) ( ( 1 − x ) 2 x ) + ( ( 1 − x ) 3 x 2 + x ) ( 1 − x x ) = ( 1 − x ) 4 x 3 + 4 x 2 + x .
∑ n = 1 ∞ n 4 x n = ∑ j = 1 ∞ ∑ n = j ∞ n 3 x n = 1 − x 1 ∑ j = 1 ∞ j 3 x j + ( 1 − x ) 2 3 x ∑ j = 1 ∞ j 2 x j + ( 1 − x ) 3 3 ( x 2 + x ) ∑ j = 1 ∞ j x j + ( 1 − x ) 4 x 3 + 4 x 2 + x ∑ j = 1 ∞ x j =
= ( 1 − x 1 ) ( ( 1 − x ) 4 x 3 + 4 x 2 + x ) + ( ( 1 − x ) 2 3 x ) ( ( 1 − x ) 3 x 2 + x ) + ( ( 1 − x ) 3 3 ( x 2 + x ) ) ( ( 1 − x ) 2 x ) + ( 1 − x ) 4 x 3 + 4 x 2 + x ( 1 − x x ) = ( 1 − x ) 5 x 4 + 1 1 x 3 + 1 1 x 2 + x .
g ( x ) = ∑ n = 1 ∞ n 5 x n = ∑ j = 1 ∞ ∑ n = j ∞ n 4 x n =
1 − x 1 ∑ j = 1 ∞ j 4 x j + ( 1 − x ) 2 4 x ∑ j = 1 ∞ j 3 x j + ( 1 − x ) 3 6 ( x 2 + x ) ∑ j = 1 ∞ j 2 x j + 4 ( 1 − x ) 4 x 3 + 4 x 2 + x ∑ j = 1 ∞ j x j
+ ( 1 − x ) 5 x 4 + 1 1 x 3 + 1 1 x 2 + x ∑ j = 1 ∞ x j =
1 − x 1 ( ( 1 − x ) 5 x 4 + 1 1 x 3 + 1 1 x 2 + x ) + ( 1 − x ) 2 4 x ( ( 1 − x ) 4 x 3 + 4 x 2 + x ) + ( 1 − x ) 3 6 ( x 2 + x ) ( ( 1 − x ) 3 x 2 + x ) + ( 1 − x ) 4 4 ( x 3 + 4 x 2 + x ) ( ( 1 − x ) 2 x ) + ( ( 1 − x ) 5 x 4 + 1 1 x 3 + 1 1 x 2 + x ) ( 1 − x x )
= ( 1 − x ) 6 x 5 + 2 6 x 4 + 6 6 x 3 + 2 6 x 2 + x
f ( x ) = ∑ n = 1 ∞ n 6 x n = ∑ j = 1 ∞ ∑ n = j ∞ n 5 x n = 1 − x 1 ∑ j = 1 ∞ j 5 x j + ( 1 − x ) 2 5 x ∑ j = 1 ∞ j 4 x j + ( 1 − x ) 3 1 0 ( x 2 + x ) ∑ j = 1 ∞ j 3 x j + ( 1 − x ) 4 1 0 ( x 3 + 4 x 2 + x ) ∑ j = 1 ∞ j 2 x j
+ ( 1 − x ) 5 5 ( x 4 + 1 1 x 3 + 1 1 x 2 + x ) ∑ j = 1 ∞ j x j + ( ( 1 − x ) 6 x 5 + 2 6 x 4 + 6 6 x 3 + 2 6 x 2 + x ) ∑ j = 1 ∞ x j =
1 − x 1 ( ( 1 − x ) 6 x 5 + 2 6 x 4 + 6 6 x 3 + 2 6 x 2 + x ) + ( 1 − x ) 2 5 x ( ( 1 − x ) 5 x 4 + 1 1 x 3 + 1 1 x 2 + x ) + ( 1 − x ) 3 1 0 ( x 2 + x ) ( ( 1 − x ) 4 x 3 + 4 x 2 + x )
+ ( 1 − x ) 4 1 0 ( x 3 + 4 x 2 + x ) ( ( 1 − x ) 3 x 2 + x ) + ( 1 − x ) 5 5 ( x 4 + 1 1 x 3 + 1 1 x 2 + x ) ( ( 1 − x ) 2 x ) + ( ( 1 − x ) 6 x 5 + 2 6 x 4 + 6 6 x 3 + 2 6 x 2 + x ) ( 1 − x x ) .
= ( 1 − x ) 7 x 6 + 5 7 x 5 + 3 0 2 x 4 + 3 0 2 x 3 + 5 7 x 2 + x .
Let u = 1 − x ⟹ d u = − d x ⟹
∫ 0 1 − a g ( x ) d x = ∫ 1 a u 6 u 5 − 3 1 u 4 + 1 8 0 u 3 − 3 9 0 u 2 + 3 6 0 u − 1 2 0 d u =
∫ 1 a u 1 − 3 1 u − 2 + 1 8 0 u − 3 − 3 9 0 u − 4 + 3 6 0 u − 5 − 1 2 0 u − 6 d u =
( ln ( u ) + u 3 1 − u 2 9 0 + u 3 1 3 0 − u 4 9 0 + u 5 2 4 ) ∣ 1 a = a 5 − 5 a 5 + 3 1 a 4 − 9 0 a 3 + 1 3 0 a 2 − 9 0 a + 2 4 + ln ( a )
and,
∫ 0 1 − a f ( x ) d x = ∫ 0 1 − a ( 1 − x ) 7 x 6 + 5 7 x 5 + 3 0 2 x 4 + 3 0 2 x 3 + 5 7 x 2 + x d x = − ∫ 1 a u 7 u 6 − 6 3 u 5 + 6 0 2 u 4 − 2 1 0 0 u 3 + 3 3 6 0 u 2 − 2 5 2 0 u + 7 2 0 d u = − ∫ 1 a u 1 − 6 3 u − 2 + 6 0 2 u − 3 − 2 1 0 0 u − 4 + 3 3 6 0 u − 5 − 2 5 2 0 u − 6 + 7 2 0 u − 7 d u = − ( ln ( u ) + u 6 3 − u 2 3 0 1 + u 3 7 0 0 − u 4 8 4 0 + u 5 5 0 4 − u 6 1 2 0 ) ∣ 1 a = − ( ln ( a ) + a 6 3 − a 2 3 0 1 + a 3 7 0 0 − a 4 8 4 0 + a 5 5 0 4 − a 6 1 2 0 − 6 = a 6 6 a 6 − 6 3 a 5 + 3 0 1 a 4 − 7 0 0 a 3 + 8 4 0 a 2 − 5 0 4 a + 1 2 0 − ln ( a )
⟹
∫ 0 1 − a f ( x ) − g ( x ) d x = a 6 1 1 a 6 − 9 4 a 5 + 3 9 1 a 4 − 8 3 0 a 3 + 9 3 0 a 2 − 5 2 8 a + 1 2 0 − 2 ln ( a ) = a 6 1 1 a 6 − 9 4 a 5 − 9 6 0 9 a 4 + 3 1 7 0 a 3 + 3 3 0 a 2 − 4 8 8 a + 1 1 9 − 2 ln ( a )
⟹ a 6 1 0 0 0 0 a 4 − 4 0 0 0 a 3 + 6 0 0 a 2 − 4 0 a + 1 = 0 ⟹ ( 1 0 a − 1 ) 4 = 0 ⟹ a = 1 0 1 ⟹ ∫ 0 1 0 9 f ( x ) − g ( x ) d x = 7 5 7 0 8 1 7 5 . 6 0 5 1 7 0 to six decimal places.