Areal Parabolic Centroid
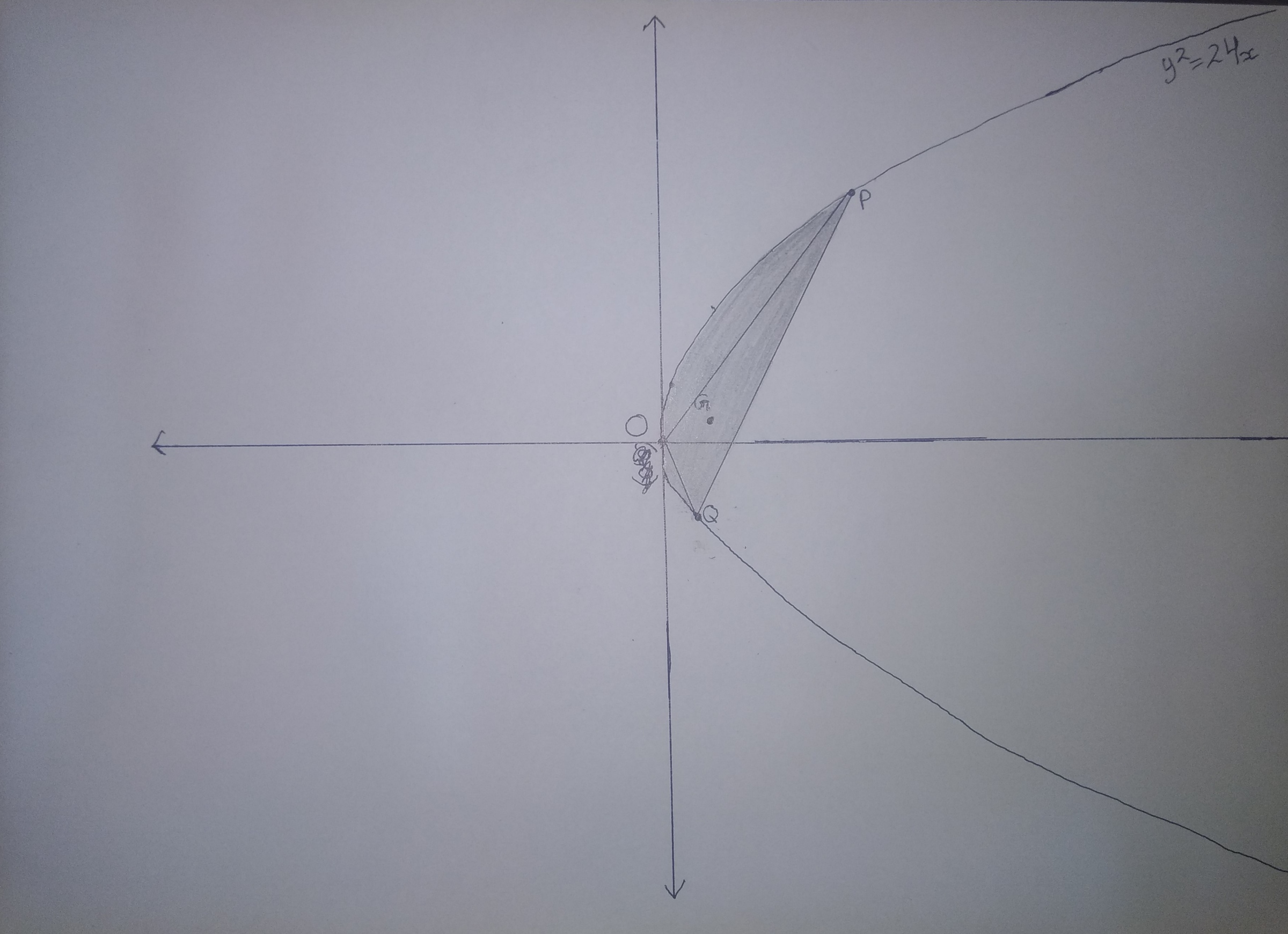
For a Parabola , consider all chords of the parabola such that the chords make a constant area with the parabola. If vertex of above parabola is , Find locus of centroid of . Length of Latus Rectum of locus if and coordinates of focus of locus is .
If , Enter answer as
Try similar problem
All of my problems are original
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Area made by chord joining P ( a t 1 2 , 2 a t 1 ) and Q ( a t 2 2 , 2 a t 2 ) of parabola y 2 = 4 a x with parabola is
A = 3 a 2 ( t 2 − t 1 ) 3
t 2 = t 1 + 3 a 2 3 A
Centroid of Δ O P Q is
G ( h , k ) ≡ ( 3 a ( t 1 2 + t 2 2 ) , 3 a ( t 1 + t 2 ) )
Putting value of t 2
G ( h , k ) ≡ ( 3 a ( t 1 2 + ( t 1 + 3 a 2 3 A ) 2 ) , 3 a ( t 1 + ( t 1 + 3 a 2 3 A ) ) )
Solving and eliminating t 1 from ( h , k ) , we get
k 2 = 3 8 a ( h − 6 a ( 3 a 2 3 A ) 2 )
So, locus is
y 2 = 3 8 a ( x − 6 a ( 3 a 2 3 A ) 2 )
So, length of latus rectum is L = 3 8 a and focus is S ( 3 2 a + 6 a ( 3 a 2 3 A ) 2 , 0 )
Putting a = 6 and for minimum x , A = 1 2
L = 1 6 , x > 5 , y = 0
So, a = 1 6 , b = 5 , c = 0 , a + b + c = 2 1