Areas?
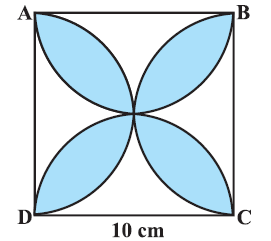 Find the area of the shaded region, where ABCD is a square of side 10 cm and semi circles are drawn with each side of the square as diameter. Take
and express your answer in
.
Find the area of the shaded region, where ABCD is a square of side 10 cm and semi circles are drawn with each side of the square as diameter. Take
and express your answer in
.
The answer is 57.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
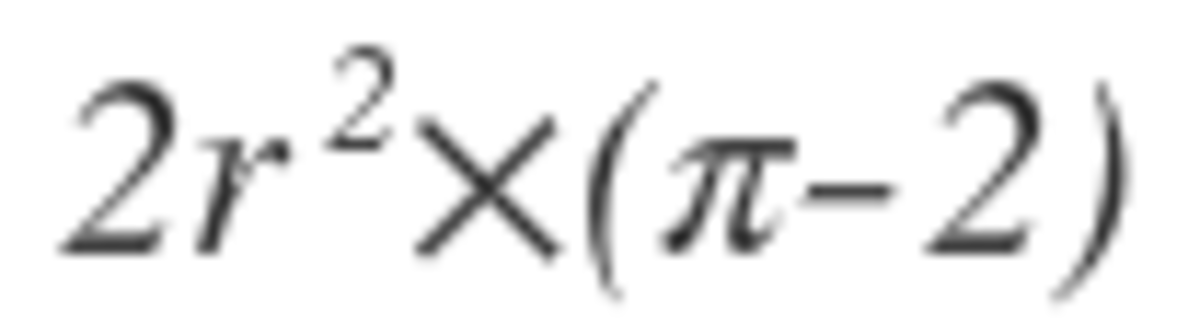
Let the center of the square be O and let the midpoint of side C D be P . Also, define R as the region bounded by the arc O C and the line segment O C . By symmetry, the area of the shaded region will be 8 times the area of R .
Now the area of R is the area of sector O P C , (a quarter-circle), minus the area of triangle Δ O P C . Thus the area of R is
4 1 π ∗ ( P C ) 2 − 2 1 ( P C ) ( O P ) = 4 2 5 ∗ 3 . 1 4 − 2 1 ∗ 2 5 = 4 2 5 ∗ ( 3 . 1 4 − 2 ) = 7 . 1 2 5 .
The area of the shaded region is then 8 ∗ 7 . 1 2 5 = 5 7 .