Areas and Circles
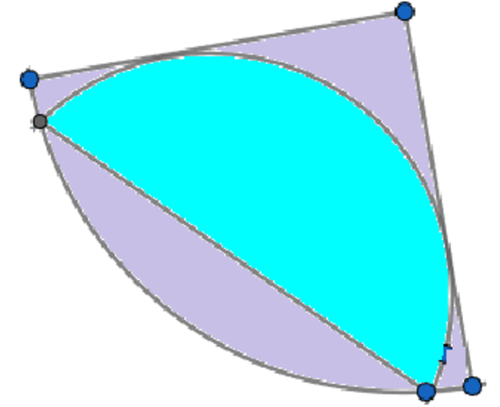
A semicircle is inscribed in a quarter of a circle of unit radius as shown in the figure. What fraction of the quarter circle is the semicircle?
The problem is not original.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let the equation of the bigger circle be x 2 + y 2 = 1 and it's center be the origin. Let the radius of the smaller circle be r and it's equation be x 2 + y 2 − 2 r x − 2 r y + r 2 = 0 . The equation of the common chord is 1 − 2 r x − 2 r y + r 2 = 0 or x + y = 2 r r 2 + 1 . Also the slope of this chord is − 1 and it passes through ( r , r ) . So it's equation is x + y = 2 r . Therefore 2 r = 2 r r 2 + 1 or r 2 = 3 1 . Hence the required ratio is 4 1 π × 1 2 2 1 π r 2 = 2 r 2 = 3 2
Put the purple area in the first quadrant, with the three vertices at ( 0 , 0 ) , ( 0 , 1 ) , ( 1 , 0 ) . Suppose the radius of the blue semicircle is r . Then the lines from the center of the blue semicircle to the tangency points on the axes must be perpendicular to those axes (because the axes are tangent). Hence those lines plus the axes make a square of side r , so the center of the blue semicircle is at ( r , r ) .
Furthermore, the diameter of the blue semicircle must have slope − 1 (the angles on the line outside the square sum to 9 0 o and must be equal by symmetry). Since the radii have length r , it's easy to compute that they contact the edge of the purple area at the points ( r − 2 r , r + 2 r ) and ( r + 2 r , r − 2 r ) . Since these points are on the unit circle, we get the equation ( r − 2 r ) 2 + ( r + 2 r ) 2 3 r 2 = 1 = 1 so r = 3 1 .
Then the blue area is 2 1 π r 2 = 6 π and the purple area is 4 π , so the ratio is 2 / 3 .
There is a solution in YouTube: https://youtu.be/PjqqoY7EmBU.
Assuming the the semicircle is symmetrically inscribed in the circular quadrant as shown. Then O R S T is a square with side length as the radius r of the semicircle. And △ O S U is a right triangle, where ∠ O S U = 9 0 ∘ . Then \by Pythagorean theorem :
O S 2 + S U 2 ( 2 r ) 2 + r 2 ⟹ r 2 = O U 2 = 1 = 3 1
Therefore A quadrant A semicircle = 4 1 π ( 1 2 ) 2 1 π r 2 = 3 2 .