Areas in a regular pentagon
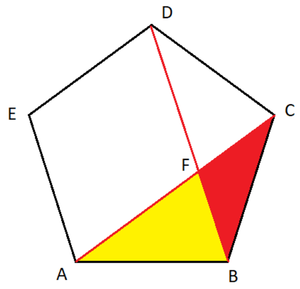
A B C D E is a regular pentagon. Segments A C and B D intersect at point F . What is the ratio of the area of △ A B F to the area of △ B C F ?
Express the answer in terms of the golden ratio , φ = 2 1 + 5 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
It is known that the ratio of a diagonal of a regular pentagon to its side is φ , hence, A C = φ .
△ A B F is isosceles , hence, A F = A B = 1 . Consequently, F C = A C − A F = φ − 1 = φ 1 .
The two coloured triangles share a common altitude from vertex B . Therefore the ratio of their areas equals the ratio of the corresponding bases:
[ B F C ] [ A B F ] = F C A F = φ 1 1 = φ .
Draw B E and let the intersection of A C and B E be G .
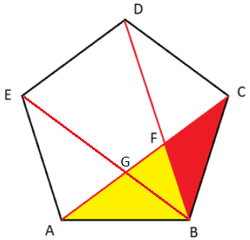
Let C F = 1 and A F = x . By symmetry, C F = B F = B G = A G = 1 , and A F = A B = B C = x .
Since △ B C F ∼ △ A C B , C F B C = A B A C , or 1 x = x x + 1 , which solves to x = φ .
Let the altitude of △ A B F and △ B C F from B be h . Then the ratio of the areas of those two triangles is A △ B C F A △ A B F = 2 1 ⋅ C F ⋅ h 2 1 ⋅ A F ⋅ h = C F A F = 1 φ = φ .
We note that E B divide △ A B F into areas [ A B G ] = a and [ B F G ] = b , where a is also the area of △ B C F . We also note that △ A B C and △ B C F are similar. Let B F = C F = 1 , then A B = B C = 2 cos 3 6 ∘ and [ B C F ] [ A B C ] = a 2 a + b = 4 cos 2 3 6 ∘ . Similarly, △ A B F and △ B F G are similar and [ B F G ] [ A B F ] = b a + b = 4 cos 2 3 6 ∘ . Then we have
a 2 a + b 1 + a a + b ⟹ a a + b = b a + b = b a + 1 = b a = φ
Since [ B C F ] [ A B F ] = a a + b = b a = φ .
Reference: golden ratio