Areas in an isosceles triangle (corrected)
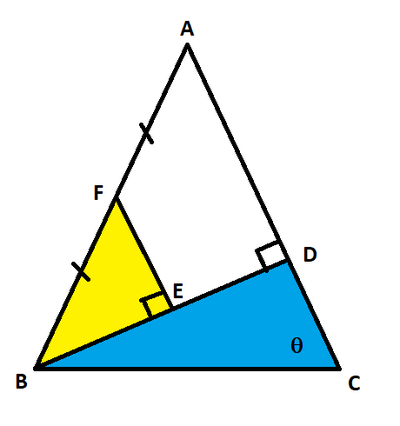
△ A B C is isosceles with A B = A C and base angle ∠ A B C = ∠ A C B = θ . B D is perpendicular to A C and F E is perpendicular to B D , where F is the midpoint of A B . If the area of △ B D C is 1 0 times the area of △ B E F , find the value of θ in degree.
Figure not drawn to scale.
The answer is 53.3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since △ B F E ∼ △ B A D by AA similarity, and since B F = F A , B E = E D .
Let x = B E = E D . Then C D = tan θ 2 x , and the area of the blue triangle is A △ B D C = 2 1 ⋅ C D ⋅ B D = 2 1 ⋅ tan θ 2 x ⋅ 2 x = tan θ 2 x 2
From the angle sum of △ C B D , ∠ C B D = 9 0 ° − θ , and since ∠ A B C = θ , ∠ F B E = ∠ A B C − ∠ C B D = θ − ( 9 0 ° − θ ) = 2 θ − 9 0 ° . From the angle sum of △ B F E , ∠ B F E = 9 0 ° − ( 2 θ − 9 0 ° ) = 1 8 0 ° − 2 θ . That means E F = tan ( 1 8 0 ° − 2 θ ) x = tan 2 θ − x , and the area of the yellow triangle is A △ B E F = 2 1 ⋅ B E ⋅ E F = 2 1 ⋅ x ⋅ tan 2 θ − x = 2 tan 2 θ − x 2 .
We are given that A △ B D C = 1 0 A △ B E F , so tan θ 2 x 2 = 2 tan 2 θ − 1 0 x 2 . Substituting tan 2 θ = 1 − tan 2 θ 2 tan θ and solving gives θ = tan − 1 ( 5 3 ) ≈ 5 3 . 3 ° .
As previously mentioned, the area of Δ A B D is 2 2 = 4 times that of Δ B E F . Therefore, Δ B D C is only 4 1 0 = 2 . 5 times larger in area than Δ A B D .
Now, since Δ A B D and Δ D B C have the same base, B D , their heights must be in the same ratio as their areas (this comes from the fact A = 2 1 b h ). Let A D = p . Then C D = 2 . 5 p . Since A B C is isoceles, A B = A C = p + 2 . 5 p = 3 . 5 p .
Using some trigonometry, tan θ = 2 . 5 p B D ⇒ B D = 2 . 5 p tan θ . We also need to find ∠ B A C which is just 1 8 0 º − 2 θ . We then use the formula A = 2 1 a b sin C for a triangle to express Δ A B D and Δ B D C in terms of θ :
Δ A B D + Δ B D C = Δ A B C 2 1 ( A D ) ( B D ) + 2 1 ( B D ) ( D C ) = 2 1 ( A B ) ( A C ) sin ( 1 8 0 º − 2 θ ) 2 1 ( p ) ( 2 . 5 p tan θ ) + 2 1 ( 2 . 5 p tan θ ) ( 2 . 5 p ) = 2 1 ( 3 . 5 p ) ( 3 . 5 p ) sin 2 θ 2 . 5 p 2 tan θ + 6 . 2 5 p 2 tan θ = 1 2 . 2 5 p 2 sin 2 θ tan θ = 1 . 4 sin 2 θ ⇒ cos θ sin θ = 2 . 8 sin θ cos θ 1 = 2 . 8 cos 2 θ ⇒ 2 . 8 1 = cos θ θ = cos − 1 ( 2 . 8 1 ) = 5 3 . 3 º .
Let the area of △ B E F be a . Since △ A B D is similar to △ B E F and its sides are twice as long, the area of △ A B D is 2 2 a = 4 a . To generalize let the area of △ B D C be n a , where n is a positive integer, then the area of △ A B C is ( n + 4 ) a .
Then the ratio of the areas [ A B C ] [ B D C ] = n + 4 n and we have:
[ B D C ] 2 1 C D ⋅ B D B C cos θ ⋅ B C sin θ B C cos θ A C B C cos θ 2 cos 2 θ cos θ ⟹ θ = n + 4 n [ A B C ] = n + 4 n ⋅ 2 1 B C ⋅ A C sin θ = n + 4 n B C ⋅ A C sin θ = n + 4 n A C = n + 4 n = n + 4 n = 2 ( n + 4 ) n = cos − 1 2 ( n + 4 ) n Note that A C B C = 2 cos θ
For n = 1 0 , we have θ = cos − 1 1 4 5 ≈ 5 3 . 3 ∘ .