Areas Inside a Rectangle
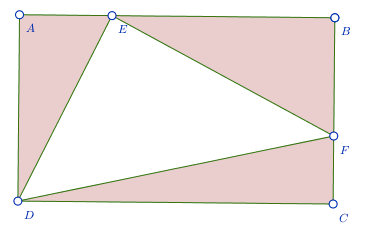 A
B
C
D
is a rectangle with point
E
on line segment
A
B
and point
F
on line segment
B
C
such that
[
A
D
E
]
=
7
,
[
B
E
F
]
=
1
1
and
[
D
C
F
]
=
9
. Then
[
D
E
F
]
=
a
b
, where
a
and
b
are integers and
b
is not a multiple of the square of any prime. What is the value of
a
+
b
?
A
B
C
D
is a rectangle with point
E
on line segment
A
B
and point
F
on line segment
B
C
such that
[
A
D
E
]
=
7
,
[
B
E
F
]
=
1
1
and
[
D
C
F
]
=
9
. Then
[
D
E
F
]
=
a
b
, where
a
and
b
are integers and
b
is not a multiple of the square of any prime. What is the value of
a
+
b
?
Details and assumptions
[ P Q R S ] denotes the area of figure P Q R S .
The answer is 56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Moderator note:
Good explanation of why we reject the negative branch.
Is it a coincidence that [ D E F ] is of the form a b ? What would the general form of [ D E F ] be?
Sorry for the delayed response. Is there a search feature for my proposed solutions?
Anyway, let's assume a more general case, with integer valued areas:
x y ( 1 − f 1 ) = a
x y f 1 f 2 = b
x y ( 1 − f 2 ) = c
And the solution f 1 = 2 c c − a − b + ( a + b − c ) 2 + 4 b c .
Let's write :
[DEF] = x y − 2 a + b + c
[ DEF ] = 1 − f 1 a − 2 a + b + c
[ DEF ] = a + b + c − ( a + b − c ) 2 + 4 b c 2 a c − 2 a + b + c
[ DEF ] = 4 a c 2 a c ( a + b + c + ( a + b − c ) 2 + 4 b c ) − 2 a + b + c
[ DEF ] = 2 ( a + b − c ) 2 + 4 b c
So the area is actually of the form 2 n k , with n , k in N . The only coincidence is that n is even.
Let A D = x , C D = y .
By following right triangle areas, we find A E = y 1 4 , B E = x − y 1 4 , B F = x − y 1 4 2 2 , and C F = x 1 8 . We have formed the equation B F + F C = A D x − y 1 4 2 2 + x 1 8 = y y x y − 1 4 2 2 x + 1 8 = x y x y − 1 4 2 2 x y + 1 8 = x y
Before proceeding, we let x y = z .
z − 1 4 2 2 z + 1 8 = z 2 2 z + 1 8 z − 1 8 ⋅ 1 4 = z 2 − 1 4 z z 2 − 5 4 z + 2 5 2 = 0 z = 2 5 4 + 5 4 2 − 4 ⋅ 2 5 2 (taking the positive root because z = [ A B C D ] ) z = 2 5 4 + 2 2 7 2 − 2 5 2 z = 2 5 4 + 2 ⋅ 3 9 2 − 2 8 z = 2 5 4 + 2 ⋅ 3 5 3 z = 2 7 + 3 5 3 This is the area of A B C D . To find [ D E F ] , we simply subtract the total area of the other triangles from z which conveniently results as 27. Thus [ D E F ] = 3 5 3 , so our answer is 5 6 .
(I'm fascinated by how easily this problem turned from geometric to algebraic. :D)
Moderator note:
You have to be careful with why you are taking the positive root. The positive root doesn't always mean "the only positive value". In this case, the negative branch of the square root gives us the value of 2 7 − 3 5 3 , which is still a positive number.
Ooh. I should I have looked out for that. Well at any route, I have to take the positive root because at the end as the area of D E F must be positive. I guess that would be more of a valid reason for taking the positive root.
Let AD = a , AE = x , CD = b , CF = y , then EB = b-x , BF = a-y .
[ADE] = 7 \Rightarrow \frac{1}{2} \times ax = 7 \Rightarrow ax = 14
[BEF] = 11 \Rightarrow \frac{1}{2} \times (a-x) (b-y) = 11 \Rightarrow ab - ax - by + xy = 22
[CDF] = 9 \Rightarrow \frac{1}{2} \times by = 9 \Rightarrow by = 18
ab - ax - by + xy = 22
ab - 14 - 18 + xy = 22
ab + xy = 54
By multiplying the two equations together, abxy = 14 \times 18 = 252
Dividing both sides with ab, we get xy = \frac{252}{ab}
By substituting, \frac{252}{ab} + ab = 54
So, we get the quadratic equation (ab)^{2} - 54ab + 252 = 0
ab = 27 \pm 3 \sqrt{53}
Because of the area of rectangle ABCD is larger that 27 square units, thus
ab = 27 + 3 \sqrt{53}
[DEF] = [ABCD] - 7 - 11 - 9
[DEF] = (27 + 3 \sqrt{53} ) - 27 = 3 \sqrt{53}
Hence, the answer is 3 + 53 = 56.
Let the length and breadth of the rectangle be a and b respectively. Let length of unknown sides for 7 and 9 area triangles be x and y respectively.
Hence, bx = 14 ay=18
(a-x) * (b-y)=ab-bx-ay+xy=22 => ab+xy=54
Now, abxy=(bx) (ay)=(ab) (xy)=14*18
Hence, ab-xy = sqrt(ab-xy)^2) = sqrt((ab+xy)^2-4*(ab)(xy)) = sqrt(54^2-4 * 14 * 18) = 6sqrt(53)
Now |DEF| = ab - 1/2(bx+ay+(a-x)(b-y)) = 1/2(ab-xy) = 3sqrt(53)
Hence, a=3, b=53; a+b=56 //
Moderator note:
That's a nice approach!
You should explain that ( a b − x y ) 2 = ( a b + x y ) 2 − 4 ( a b x y ) , which is how we obtained that line.
You can use some geometric insight to simplify the solution process.
First remember that contracting one side of a rectangle while expanding the other in the appropriate rate will keep the area invariant (the areas of the inner triangles also remain invariant).
This means you have at least one degree of freedom. Observing the 9 in the problem, I decided to use it to make C D = C F . At the same time I know I can scale the figure to have areas: 2 7 , 2 9 , 2 1 1 This because I suspect the equations will happen in the length of the sides.
Now I made my variable choice. Let A E = h (I think any other length works ) and is easy to get that: A D = h 7 , A B = 3 − h , B F = 3 − h 1 1
We obtain an equation from A D = B C that is quadratic. Solve it and you will get
h = 2 9 − 5 3
Notice that the root with positive sign is larger than 3 , so it is not a possible length for A E .
Now we obtain the area of the rectangle: A = 3 × h 7 = 9 − 5 3 4 2
And subtracting the other areas we get. 9 − 5 3 4 2 − 2 2 7
If you simplify you get 2 3 5 3 But remember the figure was scaled by a factor of 2 , this means the area of the inner original triangle is 3 5 3 , and the answer is 5 6 . ⌣ ¨
First, let's see what we have:
-
A D ∗ A E = 1 4 ⟹ ( A B − B E ) ∗ A D = 1 4 ⟹ A B ∗ A D − B E ∗ A D = 1 4
-
D C ∗ F C = 1 8 ⟹ D C ∗ ( B C − B F ) = 1 8 ⟹ D C ∗ B C − D C ∗ B F = 1 8
-
B F ∗ B E = 2 2 ⟹ ( A B − A E ) ( B C − F C ) = 2 2 ⟹ A B ∗ B C − A B ∗ F C − A E ∗ B C + A E ∗ F C = 2 2
Looking at the very last equation, we can substitute in values:
A B ∗ B C + A E ∗ F C = 5 4
Taking a look at our original equation A D ∗ A E = 1 4 and D C ∗ F C = 1 8 , we can multiply them together to get A D ∗ A E ∗ D C ∗ F C = 2 5 2 . We plug it back in to get:
A B ∗ B C + A B ∗ B C 2 5 2 = 5 4 . Solving the quadratic, we get A B ∗ B C = 2 7 + 3 5 3 . We know that the sum of the triangular areas is 2 7 , so we subtract to get 2 7 + 5 3 . Therefore our answer is 5 6 .
I meant 3 5 3 at the end.
Let A E / A B = x , and B F / B C = y , and length of the side A B = a , and that of side B C = b .
The area of the rectangle, denoted by S , is S = a b .
Then the three areas given can be expressed as three equations: x S = 1 4 , ( 1 − x ) y S = 2 2 , ( 1 − y ) S = 1 8 .
These equations can be reduced to quadratic equation for y as 7 y 2 + 1 3 y − 1 1 = 0 .
Meaningful solution is y = 1 4 − 1 3 + 3 5 3 . We can compute other unknowns: x = 6 9 − 5 3 , S = 3 ( 9 + 5 3 ) .
There are many ways one can arrive at the area [DEF]. By inspection of areas and their overlaps, we can see that [ D E F ] = [ A D E ] + [ B E F ] + E B × F C − [ D C F ] This simplifies to [ D E F ] = S ( 1 − x + x y ) / 2 = 3 5 3
This isn't the most elegant solution but it worked! Draw out rectangle ABCD, where A is the vertex in the upper left corner and B, C, D follow clockwise. Define the length and width of the rectangle to be l and w respectively and define A E = y and therefore E B =l-y). Similarly, call F C = x and therefore B F = w − x . Label D C = l and A D = w . Now we have a lot of equations we can try to bash and solve! First we have that ( l − y ) ( w − x ) = 2 2 . Expanding we get l w − l x − w y + x y = 2 2 . Whoa, that's a lot of variables. Wait! We can eliminate two of those! The area of △ A E D can be expressed as w y = 2 ( 7 ) = 1 4 . Similarly, for triangle FDC, we have x ⋅ l = 2 ( 9 ) = 1 8 . Now we have the equation l w − 1 8 − 1 4 + x y = 2 2 ⟹ 5 4 = l w + x y . Almost there! From the equations x l = 1 8 and w y = 1 4 above we can obtain that x = l 1 8 and y = w 1 4 . Now, substitute that into 5 4 = l w + x y and we get 5 4 = l w + l 1 8 ⋅ w 1 4 or 5 4 = l w + l w 2 5 2 . We can bash solve this and get that when l = 0 that w = l 3 ( 9 + 5 3 ) To cancel, let l = 3 . That means w = 9 + 5 3 . The area of ABCD is w ⋅ l = 3 ( 9 + 5 3 ) = 2 7 + 3 5 3 and now all we need to do is subtract the areas of the surrounding triangles of EFD. They just happen to sum to 2 7 so [ △ E F D ] = 3 5 3 . We have to AWIA! (Answer What Is Asked!) We have to add a = 3 and b = 5 3 to get 5 3 + 3 = 5 6 □
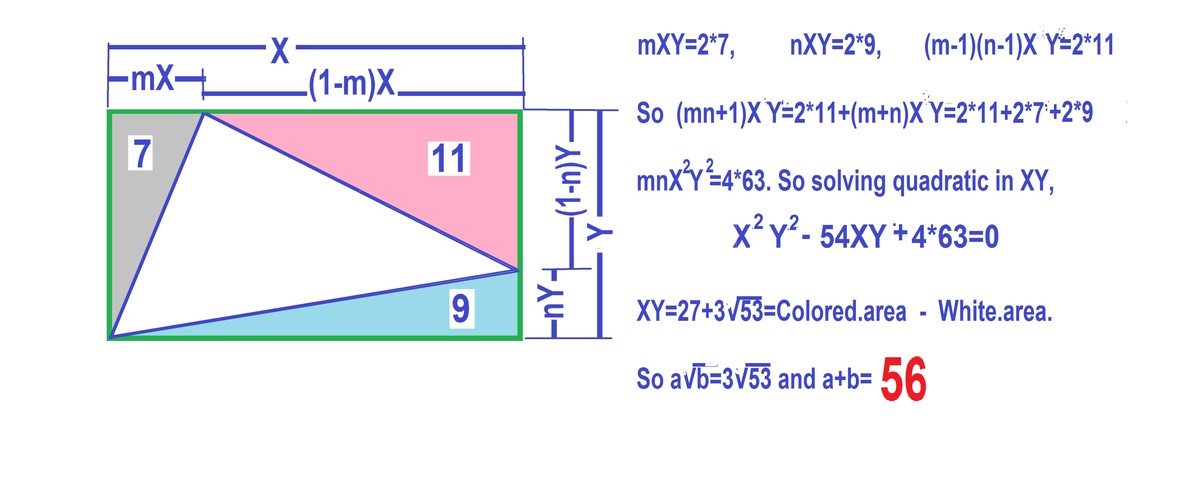
Writing the 3 areas as:
x ( y − α ) = 1 4
α β = 2 2
y ( x − β ) = 1 8
where CD = y , AD = x , BE = α , BF = β .
Rewriting α = f 1 y and β = f 2 x we obtain:
x y ( 1 − f 1 ) = 1 4
x y f 1 f 2 = 2 2
x y ( 1 − f 2 ) = 1 8
By division, we obtain :
f 1 f 2 1 − f 1 = 2 2 1 4 and 1 − f 2 f 1 f 2 = 1 8 2 2 .
From the first identity we obtain: f 2 = 1 4 2 2 f 1 1 − f 1 .
Plugging it into the second identity, we get(after simplifications):
f 1 2 + f 1 − 9 1 1 = 0
Given that f 1 is positive, we get the solution f 1 = 6 5 3 − 3 .
Using that x y ( 1 − f 1 ) = 1 4 we get that x y = 2 7 + 3 5 3 . But [ DEF ] can be expressed as x y − ( 7 + 1 1 + 9 ) . Therefore, [ DEF ] = 3 5 3 and a + b = 5 6 .