Areas made from a line and a parabola
Given the line and the parabola with . Let and be the striped areas as shown in the diagram below.
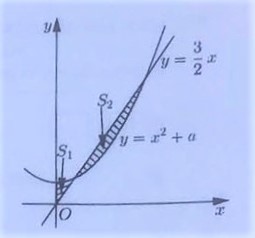
If , then in which interval must lie?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First let us calculate the intersection points between the line and the parabola, which I'll call x 1 and x 2 ( x 1 < x 2 ) :
x 2 + a = 2 3 x
2 x 2 − 3 x + 2 a = 0
x 1 = 4 3 − 9 − 1 6 a
x 2 = 4 3 + 9 − 1 6 a
The areas will be:
S 1 = ∫ 0 x 1 [ x 2 + a − 2 3 x ] d x
S 1 = 9 6 ( 7 2 a − 2 7 ) + ( 9 − 1 6 a ) 9 − 1 6 a
S 2 = ∫ x 1 x 2 [ 2 3 x − ( x 2 + a ) ] d x
S 2 = 4 8 ( 9 − 1 6 a ) 9 − 1 6 a
Making S 1 = S 2 :
7 2 a − 2 7 + ( 9 − 1 6 a ) 9 − 1 6 a = ( 1 8 − 3 2 a ) 9 − 1 6 a
7 2 a − 2 7 = ( 9 − 1 6 a ) 9 − 1 6 a
Squaring both sides:
4 0 9 6 a 3 − 1 7 2 8 a 2 = 0
Since a > 0 :
a = 4 0 9 6 1 7 2 8 = 6 4 2 7 = 0 . 4 2 1 8 7 5
So, a lies in:
( 5 2 ; 2 0 9 )