Aren't the powers too large?
 x
n
−
y
n
=
2
1
0
0
x
n
−
y
n
=
2
1
0
0
How many solutions are there to the equation above for positive integers x , y , n with n > 1 ?
Image Credit: Wikipedia Binary Number by Ephert
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
It's always the simplest case that gets me on these problems. Excellent solution! Mihalescu's Theorem can be used to take care of the case for n > 2 and even. I tried tackling the odd case with Fermat's little theorem and representing the equation as ( x n − 1 ) − ( y n − 1 ) = 2 1 0 0 , but I didn't get anywhere.
@Mehul Arora how did you solve this problem?
How do you get access to these papers?
I've put up a complete solution. Check it out!
Could you explain to me the first line?
We show a stronger result:
The equation x n − y n = 2 k , n ≥ 2 has a solution ( x , y , n , k ) in naturals iff n = 2 .
Proof: Let g = g c d ( x , y ) . Then g ∣ 2 k , so g = 2 l , for some non-negative integer l .
So take x = g p , y = g q , to get p n − q n = 2 k − l . Note that k = l ; if it was, then p n − q n = 1 , which is clearly impossible for n ≥ 2 . So k > l .
Therefore , p n − q n is even , so both p , q are odd, so 2 ∣ ( p − q ) .
This means the exceptional case of the Zsigmondy Theorem must apply, so that n = 2 and p + q = 2 m for some positive integer m .
So now 2 m ( p − q ) = ( p + q ) ( p − q ) = p 2 − q 2 = 2 k − l , so p − q = 2 k − l − m . But now, we will get 2 p = 2 m + 2 k − l − m , but p is odd, so this immediately means that 2 k − l − m = 2 . So p − q = 2 .
Therefore, we have p = 2 m − 1 + 1 and q = 2 m − 1 − 1 . This means x = ( 2 l ) ( 2 m − 1 + 1 ) and y = ( 2 l ) ( 2 m − 1 − 1 ) . But y ≥ 1 , so m ≥ 2 .
x 2 − y 2 = 2 k gives 2 l + m + 1 = k .
Here k = 1 0 0 , so 2 l + m = 9 9 . We get our 4 9 pairs ( l , m ) = ( 0 , 9 9 ) , ( 1 , 9 7 ) , . . . . , ( 4 8 , 3 ) , and the corresponding ( x , y ) .
It is obvious that we can set n to be a prime p.Lets consider the general case when 100 is replaced by m and x and y are coprime ( if they had a common divisor, it would be a power of two.But the lhs is homogenous, so we return to an equation of the previous type).The LHS is factored as follows:
( x − y ) ( x n − 1 + . . . + y n − 1 ) = 2 m
The first factor is obviously smaller than the second one, and both are powers of two, so the smaller divides the greater.But x ≡ y ( m o d x − y ) , so the second factor is congruent to n x n − 1 modulo x − y = 2 a .But we required x and y be coprime, so both are odd.That means from the last congruence that 2 a ∣ n ,n is prime.
Case 1.n is odd Here a=0 and thus x = y + 1 .We have the equation ( y + 1 ) n − y n = 2 m < ( y + 1 ) n ≤ 2 n , so n>m.But when expanding, the highest order term is n . y n − 1 , whis is less than 2 m only for y=1 by the previous argument.But this is impossible.
Case 2.n=2
This case easily leads to x = 2 m − 2 + 1 , y = 2 m − 2 − 1 .So to solve X 2 − Y 2 = 2 1 0 0 , we must have that X = 2 1 0 0 − m . x , Y = 2 1 0 0 − m . y .By a simple counting argument we arrive at the answer 49.
why do we set n to be prime?we can set n to be prime but why has n to be necessarily prime. how do you claim that no non-prime value of n will yield solns?
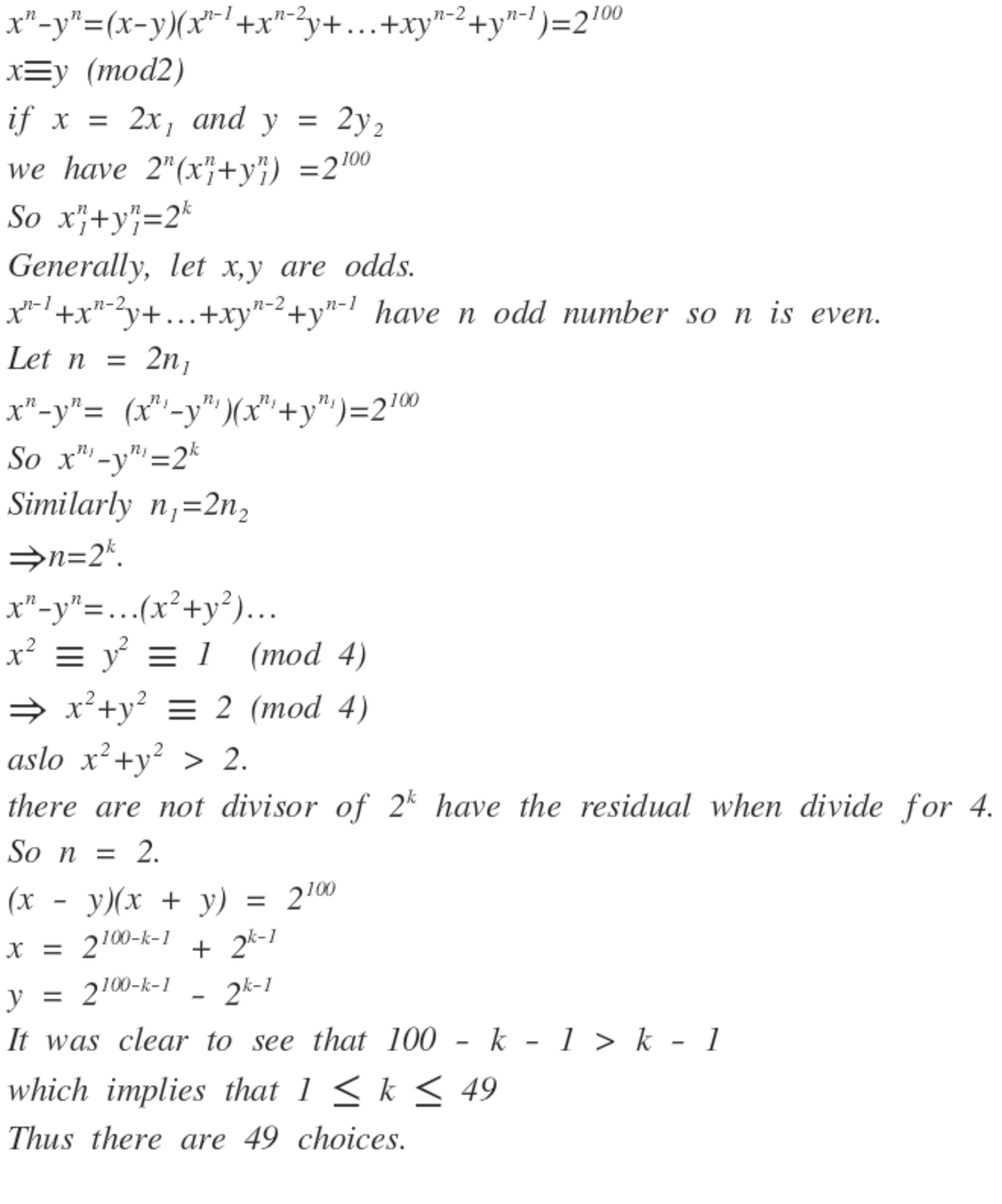
This isn't a complete solution, and I am not sure if a simple solution can be written down. By several papers due to Darmon-Merel, Bruin, Kraus, and Bennet (see references below), the equation
x n + y n = z 1 0 0
has no non-trivial solutions for n ≥ 3 . However, this is only relevant to the problem when n is odd; the even case is not covered since ( − y ) n = y n in that case. One can probably adapt the same methods however to deal with the negative sign in that situation.
If there is a particularly novel solution I would love to see it.
Anyway, if we can settle on the fact that there are no solutions when n ≥ 3 , then the rest is easy. We write x 2 − y 2 = 2 1 0 0 = ( x − y ) ( x + y ) . Then we must have x − y = 2 k , x + y = 2 1 0 0 − k . Solving the linear system, we see that x = 2 1 0 0 − k − 1 + 2 k − 1 , y = 2 1 0 0 − k − 1 − 2 k − 1 . From here we see that k − 1 < 1 0 0 − k − 1 , which implies that 1 ≤ k ≤ 4 9 . Thus there are 4 9 choices.
References:
M.A. Bennet, The equation x 2 n + y 2 n = z 5 , J. Th. Nombres Bordeaux 18 (2006), 315-321.
N. Bruin, Chabauty methods using elliptic curves, J.reine angew. Math. 562 (2003), 27-49.
N.Bruin, On powers as sums of two cubes, ANTS IV, Leiden 2000, 169- 184, Lecture Notes in Comput.Sci. 1838, Springer 2000.
H.Darmon, L.Merel, Winding quotients and some variants of Fermat’s Last Theorem, J.reine angew.Math. 490 (1997), 81-100.
A.Kraus, Sur l’´equation a3 + b3 = cp, Experiment.Math.7 (1998), 1-13.