Arithmetic Progression

Algebra Level 1

a ( q − r ) p + b ( r − p ) q + c ( p − q ) r \dfrac{a(q-r)}{p} + \dfrac{b(r-p)}{q} + \dfrac{c(p-q)}{r}

In an arithmetic progression , the sum of the first p , q , r p, q, r terms are a , b , c a, b, c respectively. Compute the expression above.


The answer is 0.

Sridhar Sri by Sridhar Sri , 25, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

6 solutions

Prasath M
Jan 12, 2016

9 Helpful 0 Interesting 0 Brilliant 0 Confused

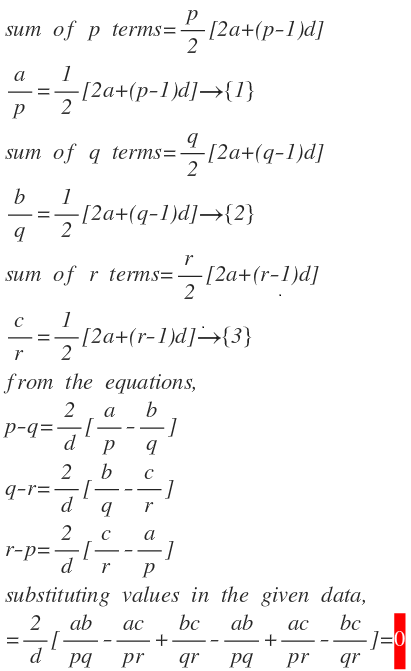
how many points for this ? 100?

Sridhar Sri - 5 years, 5 months ago

I considered a trivial case.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Ya, same here.

Pulkit Gupta - 5 years, 5 months ago
Hypergeo H.
Oct 19, 2020

To prove this for distinct p , q , r p,q,r and a , b , c a,b,c :

Note that
S n = n 2 [ 2 A + ( n − 1 ) D ] S n n = A + n − 1 2 D Δ ( S n n ) = D 2 Δ n Δ ( S n n ) Δ n = constant a p − b q p − q = b q − c r q − r a p ( q − r ) + b q ( r − p ) + c r ( p − q ) = 0 \begin{aligned} S_n &=\frac n2 [2A+(n-1)D]\\ \frac {S_n}n &=A+\frac {n-1}2D\\ \Delta \left(\frac {S_n}n\right) &=\frac D2 \Delta n\\ \frac {\Delta \left(\frac {S_n}n\right)}{\Delta n} &=\text{constant}\\ \frac {\frac ap - \frac bq}{p-q} &=\frac {\frac bq-\frac cr}{q-r}\\ \frac ap(q-r)+\frac bq(r-p)+\frac cr(p-q)=0 \end{aligned}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

There are no such rules that p,q,r are distinct, so I set p=q=r, then the answer is absolutely 0 \boxed {0}

In other way, you set a = b = c = 0 a=b=c=0 , it will get 0 \boxed {0} also.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

nice. it will be helpful for JEE

A Former Brilliant Member - 1 year, 1 month ago
Sayan Das
Jun 20, 2016

I solved exactly in that way .But after solving, I thought it could be guessed so easily

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Zeeshan Ali
Jan 13, 2016

How did I deal with the problem?

I just assumed a very simple Arithmetic Progression as under: 1 , 2 , 3 , 4 , 5 , . . . 1, 2, 3, 4, 5, . . . Now, let p, q and r be 1,2 and 3 respectively. Hence we have a=1, b=3 and c=6. Then I just put the values into the expression and got ( − 1 ) + ( 3 ) + ( − 2 ) = 0 (-1)+(3)+(-2)= \boxed{0} as outcome :)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

We cannot tell ......p,q and r can be any value...it does not always mean that p,q and r have to be in AP. They are just terms in an ap.

Adarsh pankaj - 5 years, 5 months ago

Log in to reply

Even I don't say that p, q and r are in AP. It's just a coincidence. More over the given problem is general which means any sequence can satisfy the conditions given hence I took the series for easiness :)

Zeeshan Ali - 5 years, 5 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...