Secant of an elipse for a parameter
A line p is a secant of an elipse e for all k 's from which of the following sets?
p : 2 x + 3 y − 2 k = 0 , e : 2 x 2 − 8 x + y 2 + 2 y = 0
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Is the title of this problem correct? ("Arithmetic series problem")
No, thanks. I guess I wanted to make a different problem at first, so that may be why. :D
For p to be the secant of e, there must be two intersecting points which means that there must be two solutions to the equation and this happnes only if discriminant is greater than zero: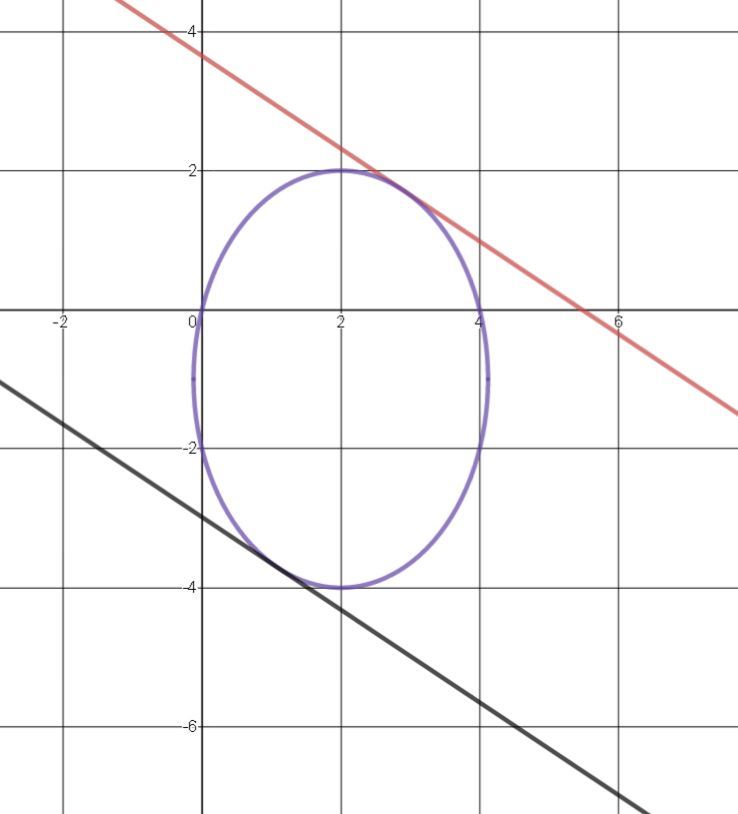
p : 2 x + 3 y − 2 k = 0 ⇒ y = 3 2 k − 2 x e : 2 x 2 − 8 x + y 2 + 2 y = 0 2 x 2 − 8 x + ( 3 2 k − 2 x ) 2 + 2 ⋅ ( 3 2 k − 2 x ) = 0 2 x 2 − 8 x + 9 4 k 2 − 8 k x + 4 x 2 + 3 4 k − 4 x = 0 1 8 x 2 − 7 2 x + 4 k 2 − 8 k x + 4 x 2 + 1 2 k − 1 2 x = 0 2 2 x 2 − 8 4 x − 8 k x + 4 k 2 + 1 2 k = 0 2 2 x 2 − x ⋅ ( 8 4 + 8 k ) + ( 4 k 2 + 1 2 k ) = 0 D = ( 8 4 + 8 k ) 2 − 4 ⋅ 2 2 ⋅ ( 4 k 2 + 1 2 k ) D = 7 0 5 6 + 1 3 4 4 k + 6 4 k 2 − 3 5 2 k 2 − 1 0 5 6 k D = − 2 8 8 k 2 + 2 8 8 k + 7 0 5 6 D > 0 − 2 8 8 k 2 + 2 8 8 k + 7 0 5 6 > 0 1 8 k 2 − 1 8 k − 4 4 1 < 0 k 1 , 2 = 3 6 1 8 ± 1 8 2 − 4 ⋅ 1 8 ⋅ ( − 4 4 1 ) = 3 6 1 8 ± 3 2 0 7 6 = 3 6 1 8 ± 5 4 1 1 = 2 1 ± 3 1 1 k ∈ ( 2 1 − 3 1 1 ; 2 1 + 3 1 1 )