Arithmetic Triangle

Let us consider the sum of all numbers in $k$ th row.

$\begin{array} {ll} s_1 = 1 \\ s_2 = 2+2 = 4 & \implies s_2 - s_1 = 3 \\ s_3 = 3+4+3 = 10 & \implies s_3 - s_2 = 6 \\ s_4 = 4+7+7+4 = 22 & \implies s_4 - s_3 = 12 \\ \cdots = \cdots \end{array}$

We note that for $k \ge 1$ ,

$\begin{aligned} s_{k+1} - s_k & = 3(2^{k-1}) \\ \sum_{k=1}^n \left(s_{k+1} - s_k\right) & = \sum_{k=1}^n 3(2^{k-1}) \\ s_{n+1} - s_1 & = 3\left(2^n-1\right) \\ \implies s_n & = 3\left(2^{n-1}\right) - 2 \end{aligned}$

Then the sum of all numbers in a 20-row triangle is:

$\begin{aligned} S & = \sum_{n=1}^{20} s_n = \sum_{n=1}^{20} \left(3\left(2^{n-1}\right) - 2\right) = 3 \sum_{n=0}^{19} 2^n - \sum_{n=1}^{20} 2 \\ & = 3 \left(\frac {2^{20}-1}{2-1}\right) - 2(20) = \boxed{3145685} \end{aligned}$

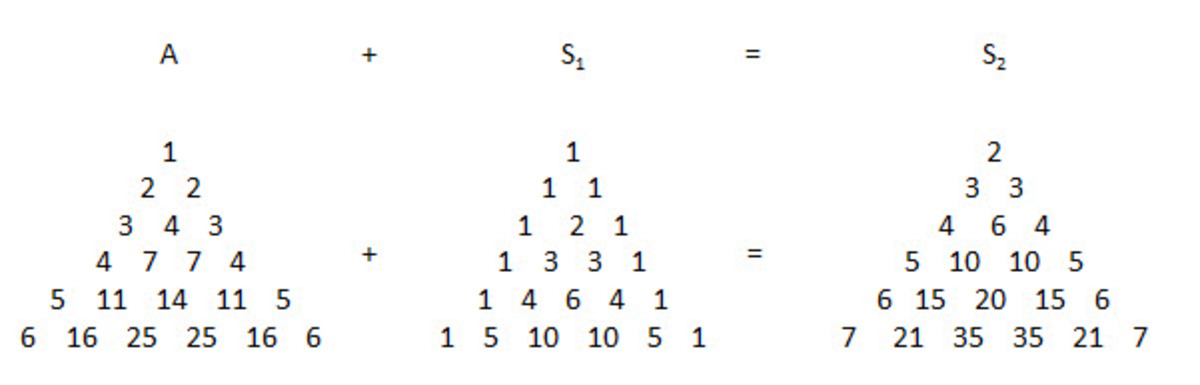
Bears some semblance to matrices... Note: continue to row 20

$A = S_{2} - S_{1} = \sum_{n=2}^{21} (2^{n} - 2) - \sum_{n=0}^{19} 2^{n} = \boxed{3145685}$

The triangle is "Pascal-like": the elements at the ends of row $n$ have value $n$ ; the other elements are the sum of the two elements above them.

It's well-known that the sums of the rows of Pascal's triangle are powers of $2$ ; so it's worth looking at row sums here (clearly this would help solve the problem). The row sums for this triangle are $1,4,10,22,46,94,\ldots$ . A bit of pattern-spotting leads us to conjecture that each row sum is $2$ more than twice the previous one - $10=2+2\times 4$ , $22=2+2\times 10$ , etc.

We could just assume this works and quickly get to the answer; but where's the fun in that?

If we want to prove this relationship, it'll help to introduce some notation. Say the $r^{th}$ element of the $n^{th}$ row is $T(n,r)$ , where $1\leq r \leq n$ (this is slightly different from the typical numbering used for Pascal's triangle, but avoids a bit of messiness).

The triangle is then defined by $T(n,1)=T(n,n)=n$ and $T(n,r)=T(n-1,r-1)+T(n-1,r)$ for $2\leq r \leq n-1$ .

Let $R(n)=\sum_{r=1}^n T(n,r)$ be the $n^{th}$ row sum.

We have

$\begin{aligned} R(n) &=\sum_{r=1}^n T(n,r)\\ &=T(n,1)+\left[ \sum_{r=2}^{n-1} T(n,r) \right]+T(n,n)\\ &=2n+\sum_{r=2}^{n-1} (T(n-1,r-1)+T(n-1,r))\\ &=2n+\sum_{r=1}^{n-2} T(n-1,r)+\sum_{r=2}^{n-1} T(n-1,r)\\ &=2n+T(n-1,1)+T(n-1,n-1) + 2\sum_{r=2}^{n-2} T(n-1,r)\\ &=2n+T(n-1,1)+T(n-1,n-1) + 2\sum_{r=1}^{n-1} T(n-1,r) - 2(T(n-1,1)+T(n-1,n-1))\\ &=2n-2(n-1) + 2R(n-1)\\ &=2+2R(n-1) \end{aligned}$

so our conjecture does indeed hold. We can now just calculate the first twenty row sums, or solve the recurrence relation $R(n)=2+2R(n-1)$ with the initial condition $R(1)=1$ to get $R(n)=3\cdot 2^{n-1} - 2$ and sum this geometric series.

Either way, we find the sum $\boxed{3145685}$ .

Ok let change it in binary. I have found a beautiful symmetry. I will right the sum of individual array in binary.

See,

$1=(1)_2$ ,

$2+2=(100)_2$ ,

$4+3+4=(1010)_2$ ,

$4+7+7+4=(10110)_2$ ,

$5+11+14+11+5=(101110)_2$ ,

$6+16+25+25+16+6=(1011110)_2$ .

So, the inner $1$ s are increasing with increase in the array.

Hence, $S_k=2^n+2^{n-1}-2$ , where $S_k$ is the sum of numbers of the $k$ th row. Hence, Total sum is easy to find.

The sum of the full triangle with $n$ rows is therefore $A_n=2^{n+1}+2^n-2n-3$ .

Put, $n=2, A_2=5$ ; $n=3, A_3=15$ ....so, the formula is perfect.

The recursive expression for the sum of any given row is:

$\large \displaystyle a_1 = 1$

$\large \displaystyle a_n = a_{n-1} + 3\cdot 2^{n-2}$

After a little work with Z-transform , one gets the general expression for $a_n$ :

$\color{#20A900} \boxed{ \large \displaystyle a_n = -2 + 3\cdot 2^{n-1}}$

So, we're looking for:

$\large \displaystyle S = \sum_{n=1}^{20} a_n$

$\large \displaystyle S = -2\sum_{n=1}^{20} 1 + \frac32 \sum_{n=1}^{20} 2^n$

$\large \displaystyle S = -40 + \frac32 (2^{21} - 2)$

$\color{#3D99F6} \boxed{ \large \displaystyle S = 3145685}$

A recursive formula for the sum in the $n$ th row is given by $a_1 = 1 \\ a_{n+1}=2a_n+2$ Each number in row $n$ is a Summand of two numbers in row $n+1$ . Then add $1$ for the left and right number.

Playing around with the therms and applying the identity $\sum_{i=0}^p 2^i= 2^{p+1}-1$ , we find $a_n=2^n+2^{n+1}-2$ and $\sum_{n=1}^ka_n=2^{k+1}+2^k-2k-3$ and thus $\boxed{2^{21}+2^{20}-2\cdot 20-3=3145685}$