Around And Around
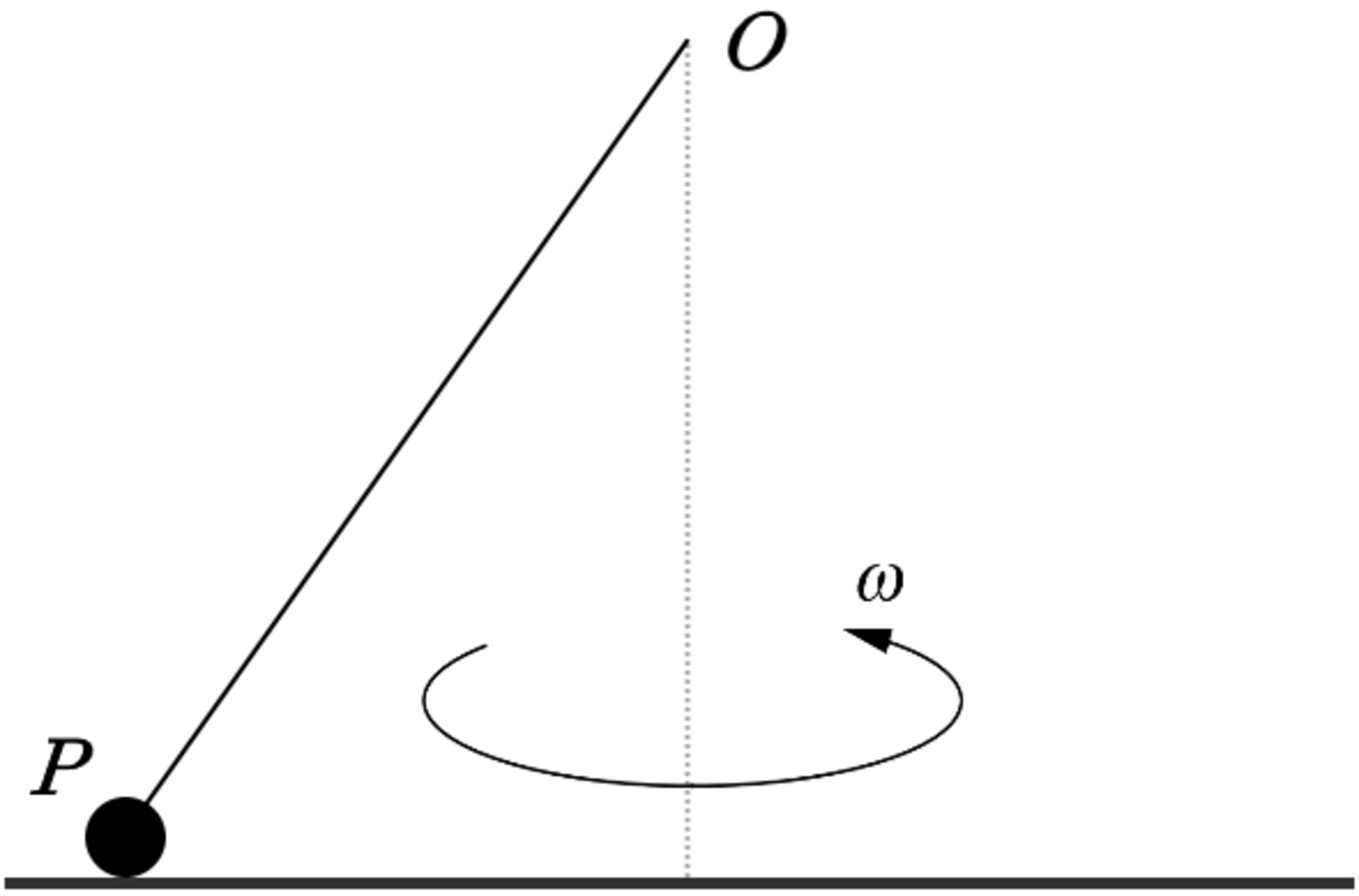 A particle
is attached to a fixed point
, which is
above a smooth horizontal plane, by a light inextensible string of length
.
A particle
is attached to a fixed point
, which is
above a smooth horizontal plane, by a light inextensible string of length
.
The particle moves in a circle with angular speed . Given that stays in contact with the plane, find the maximum value of .
Note : Let .
The answer is 12.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let G be the point exactly below O.
l ( O G ) = 0 . 8 , l ( O P ) = 1 → l ( P G ) = 6
Let the angle made by the string with the horizontal be θ , tension in the string be T , normal reaction from fround be N.
T cos ( θ ) = m l ( P G ) ω 2
T sin ( θ ) + N = m g
∴ N = m g − m l ( P G ) tan ( θ ) ω 2
Since it remains in contact,
N ≥ 0
ω 2 ≤ l ( P G ) tan ( θ ) g = 0 . 8 9 . 8 = 1 2 . 2 5