Around Corner
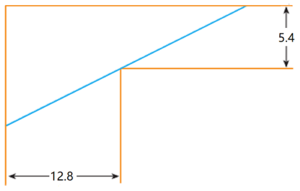
A steel pipe is being carried down a hallway 12.8 ft wide. At the end of the hall there is a right-angled turn into a narrower hallway 5.4 ft wide.
What is the length (in ft) of the longest pipe that can be carried horizontally around the corner?
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let θ be the (acute) angle the pipe makes with the horizontal. Dividing the pipe into two sections at the point of contact with the corner of the hallway, we see that the length L of the pipe is L = 1 2 . 8 sec θ + 5 . 4 csc θ . Differentiating with respect to θ gives us that d L / d θ = 1 2 . 8 sec θ tan θ − 5 . 4 csc θ cot θ , which equals 0 when
cos 2 θ 1 2 . 8 sin θ = sin 2 θ 5 . 4 cos θ ⟹ tan 3 θ = 1 2 . 8 5 . 4 = 6 4 2 7 ⟹ tan θ = 4 3 .
As L can be made as long as we'd like this extrema must represent a minimum. So as tan θ = 4 3 ⟹ sec θ = 4 5 , csc θ = 3 5 , the desired length of the longest pipe that can be carried around the corner is
L = 1 2 . 8 × 4 5 + 5 . 4 × 3 5 = 1 6 + 9 = 2 5 .