Arpit's awesome averages

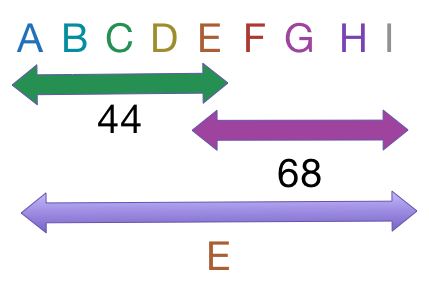1. Let the nine numbers in increasing order be a, b, c, d, e, f, g, h, i .
2. The middle number is e .
3. Since the average of the nine numbers equals their middle number e , then: > $\frac{a+b+c+d+e+f+g+h+i}{9} = e$ > $a+b+c+d+e+f+g+h+i=9e$
4. The average of the five largest values (e, f, g, h, i) equals 68 .
   > Which means that $\frac{e+f+g+h+i}{5} = 68$ > $e+f+g+h+i = 68 \times 5 = 340$
   
5. By following the same steps with the five smallest values, we get : > $a+b+c+d+e = 220$
6. By adding the last two equations : > $a+b+c+d+2e+f+g+h+i=560$
7. By combining this equation with the first one : > $9e+e=560$ > $10e=560$ > $e=56$
8. The sum of the nine numbers equals 9e, so we can get it by multiplying 9 by 56. Or, to make things easier, we can just subtract 56 from 560. The answer is 504 .

At first we should find out the middle number.
$\frac{68\times 5 + 44\times 5}{10}$ = $56$
so $56$ is the middle number .
It is in the average of largest numbers & average of largest numbers. So we should subtract $56$ from one of the average.
so the sum of first $5$ numbers is $44\times 5$ = $220$
and the sum of last $4$ numbers is $68\times 5 - 56$ = $340 - 56$ = $284$
SO,The sum of nine numbers is $284+220$ = $\boxed{504}$

Let the sum of first four numbers be $a$ , the middle number be $b$ and sum of last four numbers be $c$

Then $\frac{a+b+c}{9} = b \Rightarrow a+b+c = 9b \ldots eqn(i)$

Now $\frac{b+c}{5} = 68 \Rightarrow b+c = 340 \Rightarrow c = 340-b$

Similarly, $\frac{a+b}{5} = 44 \Rightarrow a+b = 220 \Rightarrow a = 220-b$

Hence $a+b+c = (220-b) + b + (340-b) = 560-b \ldots eqn(ii)$

Now from $eqn(i)$ and $eqn(ii)$ ,

$a+b+c = 9b = 560 - b \Rightarrow b = 56$

Therefore the answer is $a+b+c = 9\times56$ or $560-56 =$ $[504]$

Let the numbers be $x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}$

Firstly $\frac{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}+x_{7}+x_{8}+x_{9}}{9}={x_{5}}.....(1)$

Secondly $\frac{x_{5}+x_{6}+x_{7}+x_{8}+x_{9}}{5}={68}$

i.e. $x_{5}+x_{6}+x_{7}+x_{8}+x_{9}={340}.....(2)$

Thirdly $\frac{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}}{5}={44}$

i.e $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}={220}.....(3)$

From.....(2) $x_{6}+x_{7}+x_{8}+x_{9}={340-x_{5}}$

Substituting into.....(1) we get $\frac{220+340-x_{5}}{9}={x_{5}}$

i.e. $\frac{560-x_{5}}{9}={x_{5}}$

which simplifies to $10x_{5}={560}$

and $x_{5}={56}$

Hence the sum of the nine numbers is $9\times{x_{5}}=9\times56$

Which is $\boxed{504}$

First of all, if the average of nine numbers $a, b, ... i$ is the middle number $e$ , then the average of all numbers except the middle number is also $e$ . This implies that $a+b+c+d+f+g+h+i=8e$ .

Also, the average of the five smallest numbers is 44; thus, $a+b+c+d+e=220$ . Similarly, since the average of the five largest values is 68, we have $e+f+g+h+i=340$ .

Adding the two previous equations gives $a+b+c+d+2e+f+g+h+i=8e+2e=560$ , which means $10e=560 \Rightarrow e=56$ and thus the sum of the nine numbers is $9e=504$ .

sum+x=5(68+44)=560 9x+x=560 x=56 sum=9x=9(56)=504

Sum of last 5 numbers=5*Average of last 5 numbers

Sum of last 5 numbers=5*68=340

Sum of first 5 numbers=5*Average of first 5 numbers

Sum of first 5 numbers=5*44=220

Sum of first 5 numbers+Sum of last 5 numbers=560=Sum of all the numbers+Sum of the middle number which has been counted twice

Since the middle number is itself the average, adding it to the sum of all the numbers wont change the average...

Thus average is 560/10=56...

Sum of the 9 numbers is 56*9

Answer:: 504

Let the numbers be -

$a_9 > a_8 > a_7 > a_6 > a_5 > a_4 > a_3 > a_2 > a_1$

$$

Therefore , the average of the numbers

$= \dfrac{ \sum_{i=1}^{9} a_i}{9} = a_5$

$\Rightarrow \sum_{i=1}^{9} a_i = 9a_5$

Given that - $\dfrac{ \sum_{i=5}^{9} a_i}{5} = 68$

and $\dfrac{\sum_{i=1}^{5} a_i}{5} = 44$

Hence by adding the two equations ,

$\dfrac{(\sum_{i=1}^{9} a_i) + a_5 }{5} = 112$

$\Rightarrow \dfrac{ 9a_5 + a_5 }{5} = 112$

$\Rightarrow 10a_5 = 560 \Rightarrow a_5 = 56$

Thus , average of the numbers

$= \sum_{i=1}^{9} a_i = 9a_5 = 9 \times 56 = \boxed{504}$

Cheers!

We are given that the average of the nine numbers is equal to the middle integer, the average of the five largest (middle and the four higher ones) numbers is 68, and the average of the five smallest (middle and the four lower ones) numbers is 44. Since the four higher integers don't matter in terms of value when compared to each other, let them all be equal to $b$ . Same thing with the four lower integers, let them be $a$ . Finally, let the middle integer be $x$ .

Now, we can put things into algebraic expressions. We have:

$4a+x+4b=9x$

$x+4b=68\times5=340$

$x+4a=44\times5=220$

We can simplify the first equation, $4a+4b+x=9x$ .

$4a+4b=8x$

$a+b=2x$

By the second and third equations, we have

$x+4b=68\times5=340$ and $x+4a=44\times5=220$

Subtracting the second from the first, we have

$4b-4a=120$

$b-a=30$

$b=a+30$

Substituting $a+30$ into $b$ , we have (from the first equation)

$a+(a+30)=2x$

$2a+30=2x$

$x=a+15$

Now, from $x+4a=220$ , the third equation, we have $a+15+4a=220$

Solving for $a$ , we have

$5a+15=220$

$5a=205$

$a=41$

Now, we find $x$ .

$x=a+15=41+15=56$

Since the average of all nine numbers is $x$ , the sum of the numbers is $9x$

$9x=56\times9=\boxed{504}$

let the numbers in increasing order are a, b, c, d, e, f, g, h, i. (e+f+g+h+i)/5= 68. f+g+h+i= 340-e ----(1)

(a+b+c+d+e)/5= 220-e -----(2)

(a+b+c+d+e+f+g+h+i)/9= e put the values of (a+b+c+d)&(f+g+h+i) from (1)&(2) e=56

and sum =504

Average of first quartile is 44. Average of third quartile is 68. Hence, average of second quartile, which is also the midpoint, is (44+68)/2 = 56.

At this point, we don't know yet the pattern of the number, but if we calculate the difference between: the second quartile and third quartile, (56 x 68)/2 = 62, the second quartile and first quartile, (56 x 44)/2 = 44,

and then putting the numbers on a list, we can notice the common difference, which is 6. Hence, by evaluating all the unknown numbers from first term until ninth term, sum it up, we get 504.

Other than that, we also can use the formula of arithmetic progression. Try it, tho.

The sum of the first 5 numbers is 220, and the sum of the second 5 numbers is 340. Adding those together, we get 560. 560 is the sum of 10 numbers because the fifth number is included twice, so we find the average to be 56. Because adding the average to a set does not change the average, we know that the fifth number is 56. We can then subtract this from the ten-number set that sums to 560 to get 504.

If the sequence is: $a_1, a_2, ..., a_9$ .

$\sum_{i=1}^{9}a_i = 9 * a_5 (i)$

$\sum_{i=1}^{5}a_i = 5 * 44 (ii)$

$\sum_{i=5}^{9}a_i = 5 * 68 (iii)$

It's easy to see that $(i)$ could be obtained from $(ii)$ and $(iii)$ in this way:

$\sum_{i=1}^{9}a_i = \sum_{i=1}^{5}a_i + \sum_{i=5}^{9}a_i - a_5$

$9 * a_5 = 5 * 44 + 5 * 68 - a_5$

$a_5 = 56$

Then the answer is $\sum_{i=1}^{9} = 9 * a_5 = \boxed{504}$

the 9 numbers is a, b, c, d, e, f, g, h and i a+b+c+d+e = 5.44 = 220 e+f+g+h+i= 5.68 = 340 a+b+c+d = 220-e f+g+h+i = 340-e

a+b+c+d+e+f+g+h+i=9.e (220-e)+e+(340-e)=9e 560-e+e-e=9e 560-e=9e 560=9e+e 560=10e e=56

e is 56, so a -i: 52, 53, 54, 55, 56, 57, 58, 59, 60 that will be 504 of sum all of them.

Let the sum of smallest four numbers be x, the middle number be m, and the sum of the four largest numbers be y. Given that the average of numbers is middle number, i.e.
$\frac{x+m+y}{9} = m$ so, $x+y=8m$ ...........(1)
Also given that average of smallest 5 numbers is 44 i.e.
$\frac{x+m}{5} = 44$
so, $x+m = 220$ .......(2)
Also given that the average of largest 5 numbers is 68 i.e.
$\frac{m+y}{5}=68$ So, $m+y=340$ ......(3)
Adding equations 2 and 3;
$x+y+2m=560$
Putting value of x+y from equation 1
$10m=560$
$m=56$ Now, by using value of m in equations 2 and 3 we get $x=164$ and $y=284$ respectively.
Therefore, sum of nine numbers is $x+m+y = 164+56+284 = \boxed{504}$

Let the ordered numbers be represented by $a_{1},a_{2},a_{3},\dots,a_{9}$ .

Let $A=a_{1}+a_{2}+a_{3}+\dots+a_{9}$ . Let $A_{1}=a_{1}+a_{2}+a_{3}+\dots+a_{5}$ Let $A_{2}=a_{5}+a_{6}+a_{7}+\dots+a_{9}$ .

$\frac{A_{1}}{5}=44$ , $\frac{A_{2}}{5}=68$ , and $\frac{A}{9}=a_{5}$

$A_{1}+A_{2}-\frac{A}{9}=A$ . (The left side is obtained by $A_{1}+A_{2}$ having all the numbers and an extra $a_{5}$ .)

$220+340-\frac{A}{9}=A$ . (Using the third line of equations.)

$1980+3060-A=9A$ . (Getting rid of fractions)

$10A=5040$ , $A=504$

If the numbers are in an A.P.

Let, the middle integer is $a$

And the common difference is $b$

So, the numbers are $a-4b < a-3b < a-2b < a-b < a < a+b < a+2b < a+3b < a+4b$

And the sum of first 5 integers is $(a-4b) + (a-3b) + (a-2b) + (a-b) + a = 44*5 = 220$ [The sum of all numbers of a set = Number of integer x Average]

$\implies 5a-10b=220$

$\implies a - 2b=44$ ..... i

In same process the sum of last five integer is $a+(a+b)+(a+2b)+(a+3b)+(a+4b) = 68*5=340$

$\implies a + 2b=68$ ..... ii

Solving the i and ii ..

We get the value of $a=56$

And the sum of all integer $9a=56*9 = 504$

Let $a_1,a_2,.. ,a_9$ be the increasing number. So, the sum of these numbers will be $9 \times a_5$ .

Here $\frac{a_1+a_2+a_3+a_4+a_5}{5} + \frac{a_5+a_6+a_7+a_8+a_9}{5} = 68 +44$

Or, $(a_1+a_2+…..+a_9)+a_5 = 112 \times 5$

Or, $10a_5$ =560

Thus, $a_5$ =56.

So, the answer is $56 \times 9 =504$

Let S = a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8 + a9.
We’ve S = 9 * a5 and a1 + a2 + a3 + a4 + a5 = 44 5 = 44 5 = 220 &
a5 + a6 + a7 + a8 + a9 = 68 5 = 340. Adding the last two eqns, we get: a1 + a2 + a3 + a4 + 2 a5 + a6 + a7 + a8 + a9¬ = 560 or S + a5 = 560 or S + S/9 = 560 giving S = 504