Arrangement

Probability Level 2

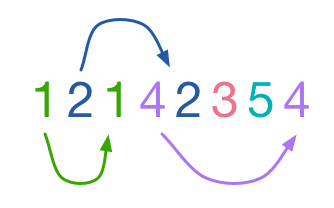
Is it possible to arrange the 3972 numbers 1 , 1 , 2 , 2 , 3 , 3 , … , 1986 , 1986 1, 1, 2, 2, 3, 3, \ldots , 1986, 1986 into one line such that there are exactly n n numbers between any two n n 's?

Yes No

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Tim Lister
Jun 21, 2016

Consider the current order of 1,1,2,2,3,3,4,4... Etc. As every n is next to its pair, the total distances between them is 0. Define a move as a swap of 2 numbers next to each other. Eg 1,1,2,3,2,3,4,4..... The total distance between pairs is now 2. ( note that the total distance can only move up and down by 2). The numbers can be positioned in any order using a series of moves so the total distance will always be even.

The desired order requires the total distance to be the 1986th triangle number. As this is odd, this makes the desired order impossible.

4 Helpful 0 Interesting 0 Brilliant 0 Confused

"The desired order requires the total distance to be the 1986th triangle number."

What does this sentence mean?

Brian Egedy - 4 years, 11 months ago

The distance between the 1's is 1, the distance between the 2's is 2, and so on. Therefore the total distance between all pairs is 1+2+3.....+1986.

Tim Lister - 4 years, 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...