Arrangement of Counters
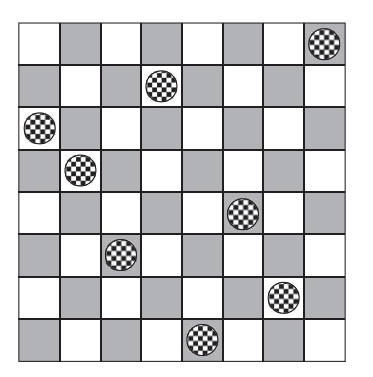
In how many ways can eight counters be placed on an 8 × 8 chessboard in such a way that no two counters lie either in the same row or in the same column?
Details and Assumptions:
- Ignore symmetry of the chessboard.
The answer is 40320.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The hours I've wasted playing Sudoku made this problem (and your solution) intuitive.
Log in to reply
Right. It does remind me of the strategy to Sudoku.
There are eight counters. Let's put it piece by piece on the board. The first piece can be placed anywhere on the board; thus we have 8 2 = 6 4 ways to do that. Now for the second counter, it can't be on the same row and column of the first counter, so we have 7 2 = 4 9 ways to do that. The third counter can't be on the same row and column of the first and second counter, so we have 6 2 = 3 6 ways to do that and so on.
total number of ways = 8 ! ( 6 4 ) ( 4 9 ) ( 3 6 ) ( 2 5 ) ( 1 6 ) ( 9 ) ( 4 ) ( 1 ) = 4 0 3 2 0
Note that we divided it by 8 ! because the order in which the counters are placed is not important.
Interesting, I didn't thought of it this way!
We place the counters in a row by row basis, so we need not to worry about placing them on the same row.
On the first row, there are 8 columns, hence 8 possibilities. On the second row, we have 7 available columns left because we cannot place it on the column that contains the first counter. The pattern continues, the total number of configurations are
8 × 7 × 6 × ⋯ × 1 = 8 ! = 4 0 3 2 0