arranging squares
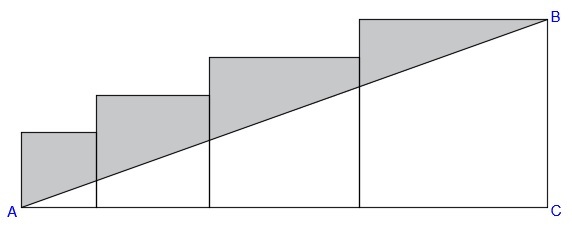 Squares with integer side lengths are arranged as shown. Right
is formed. The side lengths of the squares form an arithmetic progression with a common difference of 2. If the length of diagonal
is
, find the area of the shaded region.
Squares with integer side lengths are arranged as shown. Right
is formed. The side lengths of the squares form an arithmetic progression with a common difference of 2. If the length of diagonal
is
, find the area of the shaded region.
The answer is 76.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the side length of the smallest square be x . Then the side lengths of the other squares are x + 2 , x + 4 , and x + 6 . So the base of the right triangle is
x + x + 2 + x + 4 + x + 6 = 4 x + 1 2
By pythagorean theorem, we have
( 2 2 2 1 ) 2 = ( 4 x + 1 2 ) 2 + ( x + 6 ) 2
8 8 4 = 1 6 x 2 + 9 6 x + 1 4 4 + x 2 + 1 2 x + 3 6
1 7 x 2 + 1 0 8 x − 7 0 4 = 0
Using the quadratic formula, we get
x = 4
So the side lengths of the other squares are 6 , 8 , and 1 0 .
The area of the shaded region is equal to the total area of the squares minus the area of the triangle
A = 4 2 + 6 2 + 8 2 + 1 0 2 − 2 1 ( 2 8 ) ( 1 0 ) = 2 1 6 − 1 4 0 = 7 6