Can You Crack This Number Grid

Logic Level 2

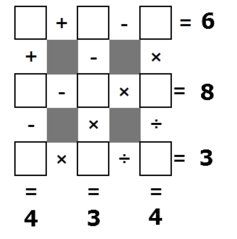Using the digits 1 through 9 without repetition, fill out the number grid above. What is the product of the numbers in the 4 corners?

Note: The order in which this grid calculates is left-to-right/top-to-bottom unlike the usual order of operations. E.g., $1+2\times 3 = (1+2)\times3=9.$

The answer is 810.

5 solutions

Chew-Seong Cheong
Aug 23, 2015

Using the same logic as Brian Charlesworth . The solution is as follows:

Why 8 - 4 x 2 = 8 ?! Must be ZERO (0)

Nguyen Nam - 4 years, 11 months ago

It is given in the problem.

Note: The order in which this grid calculates is left-to-right/top-to-bottom unlike the usual order of operations.

Chew-Seong Cheong - 4 years, 11 months ago

8-4=4 *2=8

inthiru 333 - 1 year, 1 month ago

Yes, using logic the blanks can be filled up one by one, as shown above, in the following sequence; 1,3,9,2,6,4,8,7,5.

Auro Light - 3 years, 9 months ago

Brian Charlesworth
Aug 23, 2015

Label the rows $1, 2, 3$ from top to bottom and the columns $a, b, c$ from left to right. So $(1,a)$ is the top left corner and $(3,c)$ is the bottom right. Now a step-by-step approach:

$(3,b)$ must be $1$ or $3$ since it must be a factor of $3,$ but if it were $3$ then $(3,a)$ and $3,c)$ would have to be the same. Thus $(3,b)$ is $1.$
Then $(3,a), (3,c)$ would have to be either $6,2$ or $9,3.$ But if $(3,c)$ were $2$ then $(1,c), (2,c)$ would have to be some ordering of $2,4$ or $8,1,$ which can't be since both $1$ and $2$ would have already been used. Thus $(3,a), (3,c)$ must be $9,3.$
With $(3,c)$ being $3$ we must have $(1,c), (2,c)$ being some ordering of $2,6.$ But since $(2,c)$ must be a factor of $8,$ it must be $2,$ and thus $(1,c)$ must be $6.$
Since $(2,c)$ is $2,$ we must have $(2,a) - (2,b) = 4,$ and since $1,2,3,6$ and $9$ have already been used, we are left with $(2,a) = 8$ and $(2,b) = 4.$
Plugging in $(1,a) = 5$ and $(1,b) = 7$ then satisfies all the remaining equations.

Thus the product of the corner numbers is

$(1,a) * (1,c) * (3,a) * (3,c) = 5*6*9*3 = \boxed{810}.$

Hello Sir Can you ilibrate it in a simple way...

Sufyan Baig - 1 year, 2 months ago

I have one question like this Can you solve that for me?

Sufyan Baig - 1 year, 2 months ago

Andy Boal
Jul 18, 2017

For this solution, call the digits a,b,c,d,e,f,g,h,i.

Start in the middle column, and note that b-e is a whole number and therefore h is an odd number, either 1 or 3.

Move to the bottom row. The only combinations of numbers g.h/i = 3 and satisfying h = 1 or 3 is 9, 1, 3. Therefore g is 9, h is 1 and i is 3.

We now know that c.f = 12 and that therefore they are both 2 or 6. No combination of the remaining digits can make (d-e).6 = 8 so c is 6 and f is 2.

Continuing, a+b = 12 and therefore one is 7 and the other is 5, but because we have already used the two, b must be 7, e must be 4 and a must be 5.

Finally, d = 8.

Therefore a.c.g.i = 5.6.9.3 = 810.

Good explanation. Thanks for your solution

Pi Han Goh - 3 years, 11 months ago

Thnx for xplanation

Amit Talwar - 3 years, 5 months ago

But 2nd row is confuseable

Amit Talwar - 3 years, 5 months ago

It is not after you have established that f is 2 and I will explain that at the end how we reached that. To satisfy the second row d-e should be 4 and there is only one combination that is d being 8 and e being 4. Now going back to why f is 2. In order to satisfy third column cf must be 12. There are only 4 combinations possible 3x4, 4x3, 2x6 and 6x2. First two are not possible because 3 has already been used. Now f can be either 2 or 6 but in order to satisfy the second row it should be a factor of 8 so that only leaves 2 and the rest fits in.

Zahid Hussain - 1 year, 10 months ago

Thanks for above solutions!!

SanSan Yu - 1 year, 2 months ago

Sushanth Kashyap
Aug 23, 2015

I think there is a mistake in the question. The result in the bottom right corner is not 1. Its 4.

Whoops. Fixed.

Pi Han Goh - 5 years, 9 months ago

I think its better to write answer example like a * b * c * d=answer or something like that i just answer 5693, 5 (i think input each number) and i just dont know its just mutiply all answer.

Gandhy Onlyy - 5 years, 8 months ago

6 + 2 - 2 = 6 + - *
2 - 1 * 8 = 8 - * /
4 * 3 / 4 = 3 = = =
4 3 4

Gives 192

Kelly Waters - 4 years, 3 months ago

In your solution you have only used 1,2,3,4,6 and 8 - you have to use ALL the digits from 1 to 9 and use each digit only once.

Steven Linnell - 3 years, 9 months ago

Fletcher Mattox
Jul 26, 2020

""" label the grid like this:
        a b c
        d e f
        g h i   """

from itertools import permutations
numbers = [i for i in range(1,10)]

for t in permutations(numbers):

    (a, b, c,
     d, e, f,
     g, h, i)   = t

    if ((a + b) - c == 6 and
        (d - e) * f == 8 and
        (g * h) / i == 3 and
        (a + d) - g == 4 and
        (b - e) * h == 3 and
        (c * f) / i == 4):
        print(a * c * i * g)

Can You Crack This Number Grid

The answer is 810.

5 solutions

0 pending reports