Arrowhead

Geometry Level 2

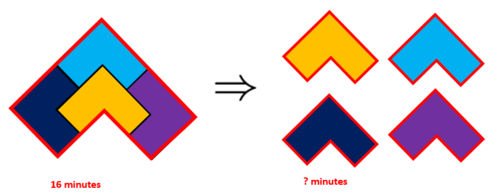It took Kevin 16 minutes to sharpen the entire edge (in red) of a large arrowhead. As pictured, 4 small arrowheads can be cut out of one large arrowhead. After cutting up the large arrow head into 4 small ones (that are each the same shape as the large arrowhead) how long will it take Kevin to re-sharpen all edges of all 4 of the small arrowheads?

Details and Assumptions

Kevin sharpens at a steady rate along the length of the edges he works on.
Even the original edges will need to be re-sharpened.

48 minutes 32 minutes 24 minutes 16 minutes

1 solution

Chung Kevin
Nov 6, 2015

Our goal is to find the perimeter of a small arrowhead, relative to the perimeter of the large arrowhead.

If 4 small arrowheads fit inside one large one that they are similar to, then the perimeter of a small arrowhead must be half of the perimeter of the large arrowhead. $16 / 2 \times 4 = 16 \times 2 = 32$ .

This is true for any two similar 2D polygons: if the perimeter of the larger polygon is $k$ -times the area of the other, then the area of the larger polygon is $k^2$ -times the area of the smaller.

Kevin divided the given red figure into $\color{#3D99F6}{\text{12 small cubes}}$ of which $\color{#D61F06}{\text{16 red sides}}$ are to be painted, it means each red side will take 1 minute.

On the similar pattern, he again divided given small shape into $\color{#3D99F6}{\text{3 small cubes}}$ , having $\color{#D61F06}{\text{8 red sides}}$ to be painted and there are total 4 small shapes to be painted.. It mean he will take $8 \times 4 = 32$ minutes.

Akhil Bansal - 5 years, 7 months ago

Arrowhead

1 solution

0 pending reports