Artillery Shell Energy Loss

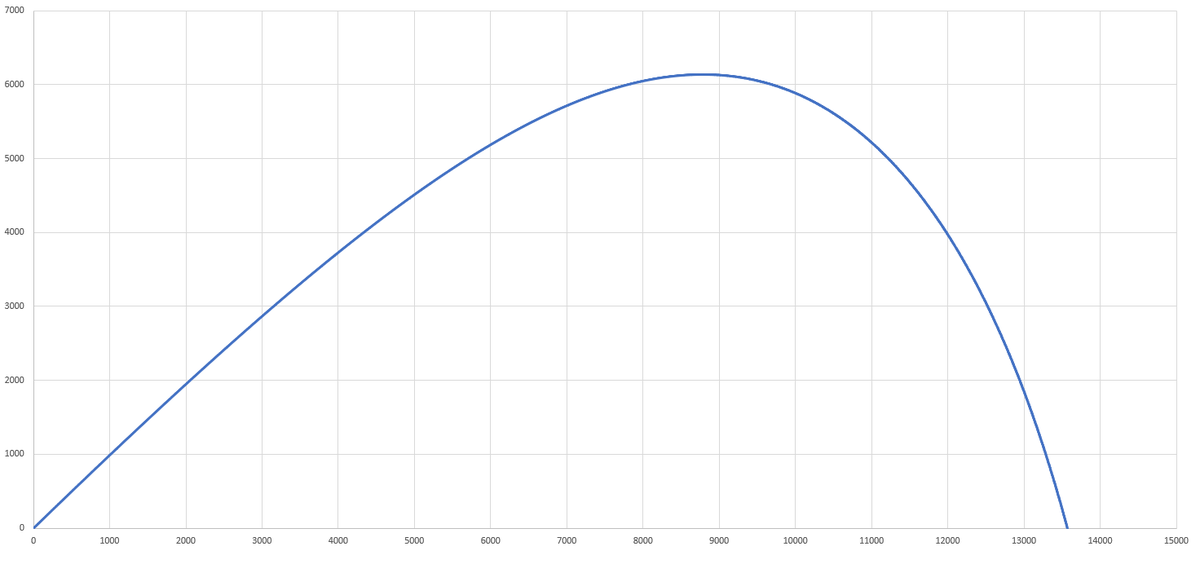
The equations of motion read:

$m\left[\begin{matrix}\ddot{x}\\ \ddot{y}\end{matrix}\right] = \left[\begin{matrix}0\\ -mg\end{matrix}\right] - \alpha \left[\begin{matrix}\dot{x}\sqrt{\dot{x}^2 + \dot{y}^2}\\ \dot{y}\sqrt{\dot{x}^2 + \dot{y}^2}\end{matrix}\right]$

This can be combined with the velocity vector to obtain a state-vector as follows. Let $x_1 = x$ , $x_2 = y$ , $x_3 = \dot{x}$ , $x_4 = \dot{y}$ . Then:

$\dot{x}_1 = x_3$ $\dot{x}_2 = x_4$ $\left[\begin{matrix}\dot{x}_3\\ \dot{x}_4\end{matrix}\right] = \left[\begin{matrix}0\\ -g\end{matrix}\right] - \frac{\alpha}{m} \left[\begin{matrix}x_3\sqrt{x_3^2 + x_4^2}\\ x_4\sqrt{x_3^2 + x_4^2}\end{matrix}\right]$

This implies:

$\left[\begin{matrix}\dot{x}_1\\ \dot{x}_2\\\dot{x}_3\\ \dot{x}_4\end{matrix}\right] = \left[\begin{matrix}x_3\\x_4\\-\frac{\alpha}{m}\left(x_3\sqrt{x_3^2 + x_4^2}\right)\\ -g-\frac{\alpha}{m}\left(x_4\sqrt{x_3^2 + x_4^2}\right) \end{matrix}\right] \implies \dot{X} = f(X)$

Initial Conditions:

$X(0) = \left[\begin{matrix}0&0&v_o\cos{\theta}&v_o\sin{\theta}\end{matrix}\right]^T$

The expression for kinetic energy is:

$T = \frac{1}{2}\left[\begin{matrix}\dot{x}& \dot{y}\end{matrix}\right] \left[\begin{matrix}m&0\\ 0&m\end{matrix}\right]\left[\begin{matrix}\dot{x}\\ \dot{y}\end{matrix}\right]$

From here, numerical integration does the job. Code attached below:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

clear all
clc

% Parameter Initialisation:
m       = 20;
vo      = 1000;
th      = pi/4;
g       = 10;
A       = 0.0025;

% Time initialisation:
dt      = 1e-5;
tf      = 75;
t       = 0:dt:tf;

% Initial conditions:
xs(:,1) = [0;0;vo*cos(th);vo*sin(th)];

for k = 2:length(t)

    % Instantaneous velocity vector:
    dx  = [xs(3,k-1);xs(4,k-1)];

    % Instantaneous acceleration vector:
    ddx = ([0;-m*g] + (-A*norm(dx)*dx))/m;

    % State vector:
    f  = [dx;ddx];

    % Explicit Euler:
    xs(:,k) = xs(:,k-1) + dt*f;

    % Checking when projectile hits ground:
    % Y-coordinate should be near zero
    if t(k) > 10 && abs(xs(2,k)) <= 1e-2
        break;
    end
end

% Kinetic energy ratio computation:
M     = m*eye(2);
V_end = [xs(3,end);xs(4,end)];
V_L   = [xs(3,1);xs(4,1)];

Ratio = (0.5*V_end'*M*V_end)/(0.5*V_L'*M*V_L)
% Ratio = 0.0638

@Karan Chatrath has provided a detailed solution. I will just add a few observations. The projectile lands with remarkably little kinetic energy (only 6 percent of its starting kinetic energy). It also has a steeper trajectory upon landing then at launch (75 degrees at landing vs. 45 at launch).

A plot of the trajectory is attached, along with simulation code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

import math

m = 20.0
v0 = 1000.0
theta = math.pi/4.0
g = 10.0
alpha = 1.0 * 0.0025


################################

E0 = 0.5*m*(v0**2.0)

dt = 10.0**(-5.0)

################################

t = 0.0

x = 0.0
y = 0.0

xd = v0*math.cos(theta)
yd = v0*math.sin(theta)

xdd = 0.0
ydd = 0.0

count = 0

while y >= 0.0:

    x = x + xd * dt
    y = y + yd * dt

    xd = xd + xdd * dt
    yd = yd + ydd * dt

    v = math.hypot(xd,yd)
    E = 0.5*m*(v**2.0)

    ux = xd/v
    uy = yd/v

    Fgx = 0.0
    Fgy = -m*g

    Fd = alpha*(v**2.0)

    Fdx = Fd*(-ux)
    Fdy = Fd*(-uy)

    Fx = Fgx + Fdx
    Fy = Fgy + Fdy

    xdd = Fx/m
    ydd = Fy/m

    t = t + dt
    count = count + 1

    if count % 1000 == 0:
        print t,x,y

################################

print ""
print ""

print dt
print t
print alpha
print ""
print x
print y
print ""
print (v/v0)
print (E/E0)
print ""
print 180.0 * math.atan(-yd/xd) / math.pi