When Orthocenter Meets Incircle

Since the triangle is isosceles, $A,I,H$ are collinear, where $I,H$ are the incenter and orthocenter respectively. Let $AH\cap BC, \odot (ABC)=D,E$ . It is well known that $DE=DH$ , thus $H$ lies on the the incircle implies $DE=DH=2ID$ . Using an incenter property from triangles - incenter , we know

$\frac {AI}{ID}=\frac {EI}{DE}=\frac {ID+DE}{DE}=\frac {3}{2}.$

Hence by the angle bisector theorem, $\frac {AB}{BC}=\frac {AB}{2BD}=\frac {AI}{2ID}=\boxed {\frac {3}{4}}$

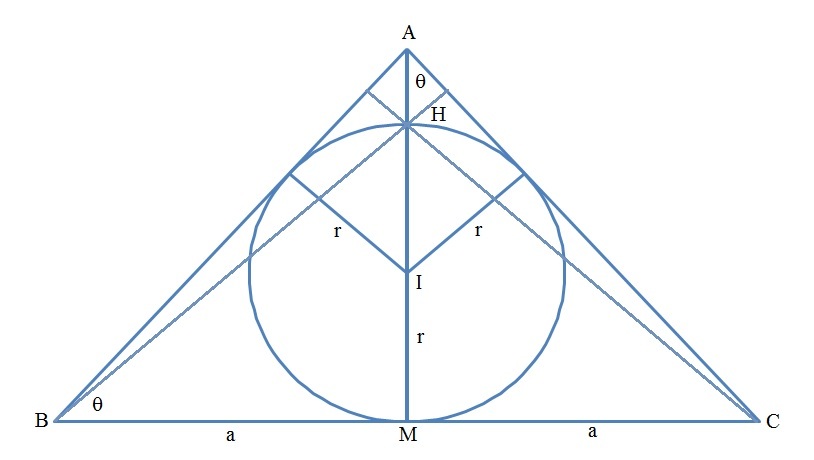
Let the orthocenter, incenter and the mid-point of $BC$ be $H$ , $I$ and $M$ respectively; the radius of the incircle be $r$ , $BM=CM=a$ and $\angle MAB = \angle MAC = \theta$ .

We note that $\angle HBM = \angle HCM = \theta$ . Then:

$\begin{aligned} \tan \theta & = \frac{HM}{BM} = \frac{2r}{a} \end{aligned}$

Also that:

$\begin{aligned} \sin \theta & = \frac{r}{AM-IM} = \frac{r}{\frac{a}{\tan \theta}-r} = \frac{1}{\frac{a}{r\tan \theta}-1} = \frac{1}{\frac{2}{\tan^2 \theta}-1} \\ & = \frac{\sin^2 \theta}{2 \cos^2 \theta - \sin^2 \theta} \\ 2 \cos^2 \theta - \sin^2 \theta & = \sin \theta \\ 2 - 3 \sin^2 \theta & = \sin \theta \\ \Rightarrow 3\sin^2 \theta + \sin \theta -2 & = 0 \\ (3\sin \theta - 2) (\sin \theta +1) & = 0 \\ \Rightarrow \sin \theta & = \begin{cases} \frac{2}{3} \\ \color{#D61F06}{-1 \quad \theta < 90^\circ \text{ rejected}} \end{cases} \end{aligned}$

Therefore $\dfrac{AB}{BC} = \dfrac{1}{\frac{BC}{AB}} = \dfrac{1}{\frac{2BM}{AB}} = \dfrac{1}{2 \sin \theta} = \dfrac{3}{4} = \boxed{0.75}$

I'm going to give two solutions. The first is done by using the Olympiad knowledge; the second is done by using coordinate geometry, from which even a junior high-school student should understand very well.

$\textbf{Solution:}$

Let $D$ and $r$ be the midpoint of $BC$ and the inradius of $\triangle ABC$ respectively. Since $AB = AC$ , the incentre $I$ , circumcentre $O$ and orthocentre $H$ all lie on the median $AD$ . Then $DI = r$ . For $H$ lying on the incircle of $\triangle ABC$ , $IH=r$ and hence $DH = DI + IH = 2r$ .

Let $AD$ produced, $BH$ produced and $CH$ produced meet $\odot(ABC)$ , $AC$ and $AB$ at $H'$ , $E$ and $F$ respectively.

By the definition of the orthocentre, $\angle CFA = \angle BEA = 90^{\circ}$ . Since $O$ lies on $AH'$ , $AH'$ is the diameter of $\odot(ABC)$ and thereby $\angle ABH' = \angle ACH' = 90^{\circ}$ . Then $BH'//CH$ and $H'C//BH$ . It follows that $BHCH'$ is a parallelogram. The diagonals $BC$ and $HH'$ meet at $D$ and therefore $H'D = DH = 2r$ .

It is well-known in the Olympiad community that $H'$ is the centre of $\odot (BIC)$ . Consequently, $BH' = IH' = ID + DH' = 3r$ . It is readily seen that $\triangle ABD \sim \triangle BH' D$ . So the proportionality gives

$\begin{aligned} && \frac{AB}{BH'} &= \frac{BD}{H'D}\\ &\Longrightarrow & \frac{AB}{BD} &= \frac{BH'}{H'D} = \frac{3r}{2r} =\frac{3}{2}\\ & \Longrightarrow & \frac{AB}{BC} & =\frac{AB}{2BD} = \frac{3}{4} = 0.75, \ \text{as required. []} \end{aligned}$

.

.

$\textbf{Alternative Solution:}$

Introduce a coordinate system such that $A=(b,h), B=(0,0), C=(2b,0)$ .

Let $M = (b,0)$ . It is clear that $AM$ is a median. Since $\triangle ABC$ is an isosceles triangle, both incentre $I$ and orthocentre $H$ lie on $AM$ .

Let $r$ be the inradius of $\triangle ABC$ . Then $I = (b,r)$ . Since $H$ lies on $AM$ and the incircle of $\triangle ABC$ , $H = (b,2r)$ .

Note that $CH \perp AB$ , by definition of the orthocentre. This means that

$\begin{aligned} m_{CH} \cdot m_{AB} &= -1\\ \frac{0-2r}{2b - b} \cdot \frac{h-0}{b-0} &=-1\\ b^2 &= 2hr\quad \quad (1) \end{aligned}$

Consider the semi-perimeter of $\triangle ABC$ : $s_{\triangle ABC} = \dfrac{2b + \sqrt{b^2 + h^2}}{2} = b^2 + \sqrt{b^2 + h^2},$ and the area of $\triangle ABC$ : $(ABC) = bh$ . As $(ABC) = rs_{\triangle ABC}$ , we have

$r =\dfrac{bh}{b + \sqrt{b^2 + h^2}} \quad \quad (2)$

Plugging $(2)$ into $(1)$ , we obtain

$\begin{aligned} b^2 &=2h \left(\frac{bh}{b + \sqrt{b^2 + h^2}}\right) & \\ 2bh^2 &= b^3 + b^2 \sqrt{b^2 + h^2} & \\ 2h^2 &= b^2 + b \sqrt{b^2 + h^2} &\text{ since } b \neq 0\\ \left(2h^2 - b^2\right)^2 &= b^4 + b^2 h^2& \\ 4h^4 - 5b^2 h^2 &=0 & \\ h^2 \left(4h^2 - 5b^2\right) &=0 & \\ h^2 &= \frac{5}{4} b^2 &\text{ since } h\neq 0 \end{aligned}$

Hence $AB = \sqrt{b^2 + h^2} = \sqrt{b^2 + \frac{5b^2}{4}} = \frac{3}{2} b$

and thus the required ratio: $\displaystyle \frac{AB}{BC} = \frac{\frac{3}{2} b}{2b} = \frac{3}{4} = 0.75$ . []

Let the foot of the perpendicular from $A$ to $BC$ be $M$ .

Let $H,I$ be the orthocentre and incentre respectively.

(I)Since in an isosceles triangle orthocentre and incentre are collinear .

Proof of statement I :

$\triangle(ABM)$ is congruent to $\triangle(ACM)$ (By $RHS$ test ) $AB=AC,AM=AM,\angle(AMB)=\angle(AMC)$

Therefore $M$ is a midpoint of $BC$ . Let $J$ be the intersection of incircle with $BC$ .

Therefore $\angle(IJC)=90°$ . $2BJ=AB+BC-AC,2CJ=BC+AC-AB$

But, $AB=AC$

Therefore $BJ=CJ,BJ+CJ=BC$ .

This implies $J$ is the midpoint of $BC$ , but we proved that $M$ is the midpoint of $BC$ .

Therefore $J,M$ must coincide.

This proves that $I$ lies on $AM$ .

Therefore $A,M,H,I$ are colinear.

Since $AB=AC$ , $\angle(B)=\angle(C)$ Now $\boxed{tan(\frac{B}{2})=\frac{IM}{BM}}.......(1)$ ) $\angle(HBC=(90-C)=(90-B)$

Therefore $tan(90-B)=\frac{HM}{BM}$

But $2IM=HM$ since $H,I,M$ are collinear and also lie on a circle with $I$ as the centre .

hence $\boxed{Cot(B)=\frac{2IM}{BM}}.......(2)$

Dividing $(1)$ by $(2)$ We get $\frac{1}{2}=tan(B)tan(\frac{B}{2})$

After solving this we get, $tan(B)=\frac{\sqrt{5}}{2}$

But $(90-\frac{A}{2})=B$ Therefore $tan(\frac{A}{2})=\frac{2}{\sqrt{5}}$

This implies $sin(\frac{A}{2})=\frac{2}{3}......(3)$

In triangle $ABM$ $sin(A/2)=BM/AB=BC/2AB....(4)$

Therefore using $(3),(4)$ we get

$\frac{AB}{BC}=\frac{3}{4}$

Let AD be the perpendicular angle bisector.we know HD=2RcosBcosC and A/Q HD=2r. Equating we get the desired result.

My solution uses the coordinates system. I used GeoGebra to present this solution. You can see it at the following link

link text

This problem is from the INMO 2016.

I suggest you to draw a diagram first.

Let angle ABC = x. let D be the foot of perpendicular from A to BC. Let I be the incentre and H be the orthocentre.

Angle IBM = x/2 , angle HBD = 90 - x.

HD = 2ID.

tan (x/2) = ID/BD. tan (90-x) = HD/BD.

This gives the value of tan (x/2), and hence the values of all other angles.