Astronaut's Momentum

Classical Mechanics Level 2

A two-stage rocket moves in space at a constant velocity of 4900 m/s. The two stages are then separated by a small explosive charge placed between them. Immediately after the explosion the velocity of the 1200 kg upper stage is 5700 m/s in the same direction as before the lower explosion. What is the velocity (in m/s) of the 2400 kg lower stage after the explosion?

The answer is 4500.

2 solutions

Chew-Seong Cheong
Nov 27, 2016

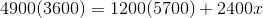
Let the masses of the upper stage and lower stage be $m_1$ and $m_2$ , their initial velocity together before the explosion be $v_0$ and their velocities after the explosion be $v_1$ and $v_2$ respectively. Then by conservation of momentum, we have:

$\begin{aligned} (m_1+m_2)v_0 & = m_1v_1 + m_2v_2 \\ \implies v_2 & = \frac {(m_1+m_2)v_0 - m_1v_1}{m_2} \\ & = \frac {(1200+2400)4900-1200(5700)}{2400} \\ & = \boxed{4500} \text{ m/s} \end{aligned}$

Zeyad Moustafa
Nov 27, 2016

Remember when solving a momentum problem that momentum is conserved. Start by setting up the following. The initial momentum (total mass times velocity) equals the momentum of the lower stage plus the momentum of the upper stage.

Astronaut's Momentum

The answer is 4500.

2 solutions

0 pending reports