Asymptotic Field Lines
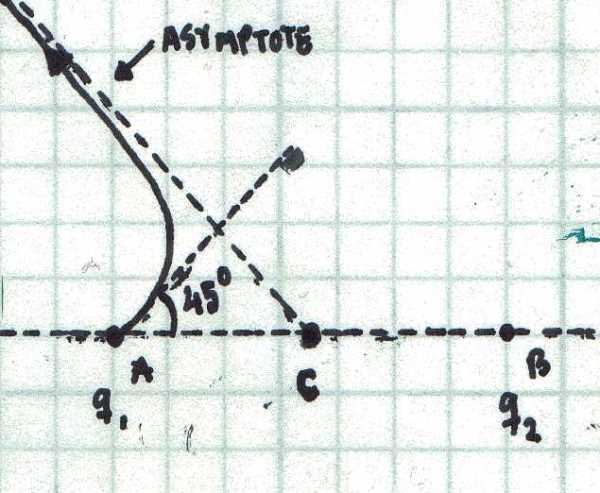
Consider two charges q 1 = 3 μ C and q 2 = 1 μ C located at points A and B, separated by a distance A B = 1 0 cm . Since both charges have the same sign, any field emanating from one of the charges will go off to infinity. It is clear, that far away from the charges, the field lines become straight lines, and therefore, they have oblique asymptotes. Consider a field line exiting the charge q 1 at α = 4 5 ∘ (as shown in the figure). Let C denote the point where the oblique asymptote corresponding to this line intersects A B . Determine the distance A C in centimeters .
The answer is 2.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice way to hit the problem! I must say, great thinking man!...
I have a question though (not with your solution, but with the question as such). What is meant by "a field line exiting the charge"? What I don't get is, what's the definition of a field line ? It's obviously not the path traced by a charge kept at a place in the field. The question doesn't make sense! (to me, of course!). Do you have any idea?
I had tried requesting a clarification , but didn't get any reply. So I had to ask here. Oh, and I am not trying to "hijack" your answer to post this question :D
Log in to reply
Sorry for a late reply Parth, I didn't notice your comment until now. About the question...
A field line is a path (a curve), whose tangent at any point gives the direction of the Electric Field at that point.
For eg, look at the diagram that I gave in my solution. Here, the vector addition of
E
1
and
E
2
gives the direction of the field at the point
(
x
,
y
)
.
Hence, according to our definition, the direction of this vector addition must give the tangent to the given curve.
If we translate these definition into the mathematical realm, then things get a bit interesting.
I assume you know a thing or two about vector fields.
Let the Vector field of a system of charges be given as :
E = f ( x , y ) i ^ + g ( x , y ) j ^
In other words, this function gives the direction and magnitude of the Electric field at any point ( x , y ) .
As we discussed, this direction must be tangent to the field line.
So,
If
y
=
ϕ
(
x
)
represents the field line, then,
d x d ϕ ( x ) = d x d y = f ( x , y ) g ( x , y )
Hence, if we have information about f ( x , y ) and g ( x , y ) , then we can form a differential equation using the above relation, which on solving, will give us the equation of the Field Line for the system of charges.
Note: Sorry for the long comment. I couldn't help but provide you some extra info.
Log in to reply
Funny that I had started along similar lines (sic!), but then I got confused somewhere in the middle. I got the vector field (which was extremely complex, no doubt!), and then I even went till writing the DE and then something happened, and kaboom!
Thanks for clearing it up! While I was typing this comment (which took around half an hour of writing-clearing-writing!), I understood all of this. My questions got answered just as I was trying to put them in words. Thanks again! :)
Considering At infinity we can assume that total charge were located at their common centre of charge and thus asymptote showing the direction of field will pass though the centre of charge 2.5 cm away from A
I did the exact same way but was very much unsure whether that would be the right answer
BTW :: Can anyone tell me why is that 45 degrees necessary
Log in to reply
According to me any field line would have done . It was just to confuse.
same here!! upvoted!
Here is a fully analytic solution. Let
θ
and
ϕ
be the angles that lines from the point
(
x
,
y
)
to the points
A
and
B
make with the
x
-axis. We have chosen
A
and
B
to lie on the
x
-axis, and have chosen the origin
O
to be the midpoint of
A
B
, so that
A
and
B
have coordinates
(
−
5
,
0
)
and
(
5
,
0
)
respectively.
 A standard result is that the equation of a field line for this problem is
3
q
cos
θ
+
q
cos
ϕ
=
q
c
for some constant
c
, where
3
q
and
q
are the charges at
A
and
B
. For this particular problem (which has
θ
=
4
1
π
and
ϕ
=
π
as initial values), we have
c
=
2
3
2
−
1
, but this is unimportant. Regarding
ϕ
as a function of
θ
, we deduce that
3
sin
θ
+
sin
ϕ
ϕ
′
=
0
Using the Sine Rule we have
r
=
sin
(
ϕ
−
θ
)
1
0
sin
ϕ
and hence
x
(
θ
)
=
sin
(
ϕ
−
θ
)
1
0
cos
θ
sin
ϕ
−
5
y
(
θ
)
=
sin
(
ϕ
−
θ
)
1
0
sin
θ
sin
ϕ
But then
x
′
(
θ
)
y
′
(
θ
)
=
=
sin
2
(
ϕ
−
θ
)
1
0
[
−
sin
θ
cos
θ
ϕ
′
+
sin
ϕ
cos
ϕ
]
=
sin
ϕ
sin
2
(
ϕ
−
θ
)
1
0
[
3
sin
2
θ
cos
θ
+
sin
2
ϕ
cos
ϕ
]
sin
2
(
ϕ
−
θ
)
1
0
[
−
sin
2
θ
ϕ
′
+
sin
2
ϕ
]
=
sin
ϕ
sin
2
(
ϕ
−
θ
)
1
0
[
3
sin
3
θ
+
sin
3
ϕ
]
and hence
(
5
+
x
(
θ
)
)
y
′
(
θ
)
−
y
(
θ
)
x
′
(
θ
)
=
sin
2
(
ϕ
−
θ
)
1
0
0
sin
2
ϕ
The tangent to the fieldline at the point
x
(
θ
)
,
y
(
θ
)
)
has equation
(
x
−
x
(
θ
)
)
y
′
(
θ
)
=
(
y
−
y
(
θ
)
)
x
′
(
θ
)
and hence meets the
x
-axis at the point
(
X
(
θ
)
,
0
)
, where
X
(
θ
)
=
y
′
(
θ
)
x
(
θ
)
y
′
(
θ
)
−
y
(
θ
)
x
′
(
θ
)
=
3
sin
3
θ
+
sin
3
ϕ
1
0
sin
3
ϕ
−
5
In the asymptotic limit, the fieldline tends towards the situation with
θ
=
ϕ
=
α
, where
4
cos
α
=
c
. It is clear that the limit of
X
(
θ
)
is
4
1
0
−
5
=
−
2
.
5
, and hence
A
C
=
2
.
5
cm.
A standard result is that the equation of a field line for this problem is
3
q
cos
θ
+
q
cos
ϕ
=
q
c
for some constant
c
, where
3
q
and
q
are the charges at
A
and
B
. For this particular problem (which has
θ
=
4
1
π
and
ϕ
=
π
as initial values), we have
c
=
2
3
2
−
1
, but this is unimportant. Regarding
ϕ
as a function of
θ
, we deduce that
3
sin
θ
+
sin
ϕ
ϕ
′
=
0
Using the Sine Rule we have
r
=
sin
(
ϕ
−
θ
)
1
0
sin
ϕ
and hence
x
(
θ
)
=
sin
(
ϕ
−
θ
)
1
0
cos
θ
sin
ϕ
−
5
y
(
θ
)
=
sin
(
ϕ
−
θ
)
1
0
sin
θ
sin
ϕ
But then
x
′
(
θ
)
y
′
(
θ
)
=
=
sin
2
(
ϕ
−
θ
)
1
0
[
−
sin
θ
cos
θ
ϕ
′
+
sin
ϕ
cos
ϕ
]
=
sin
ϕ
sin
2
(
ϕ
−
θ
)
1
0
[
3
sin
2
θ
cos
θ
+
sin
2
ϕ
cos
ϕ
]
sin
2
(
ϕ
−
θ
)
1
0
[
−
sin
2
θ
ϕ
′
+
sin
2
ϕ
]
=
sin
ϕ
sin
2
(
ϕ
−
θ
)
1
0
[
3
sin
3
θ
+
sin
3
ϕ
]
and hence
(
5
+
x
(
θ
)
)
y
′
(
θ
)
−
y
(
θ
)
x
′
(
θ
)
=
sin
2
(
ϕ
−
θ
)
1
0
0
sin
2
ϕ
The tangent to the fieldline at the point
x
(
θ
)
,
y
(
θ
)
)
has equation
(
x
−
x
(
θ
)
)
y
′
(
θ
)
=
(
y
−
y
(
θ
)
)
x
′
(
θ
)
and hence meets the
x
-axis at the point
(
X
(
θ
)
,
0
)
, where
X
(
θ
)
=
y
′
(
θ
)
x
(
θ
)
y
′
(
θ
)
−
y
(
θ
)
x
′
(
θ
)
=
3
sin
3
θ
+
sin
3
ϕ
1
0
sin
3
ϕ
−
5
In the asymptotic limit, the fieldline tends towards the situation with
θ
=
ϕ
=
α
, where
4
cos
α
=
c
. It is clear that the limit of
X
(
θ
)
is
4
1
0
−
5
=
−
2
.
5
, and hence
A
C
=
2
.
5
cm.
It doesnt matter what the angle of emmision is,,
the simple concept is to find an analogy which in this case is centre of mass, you see at large distances the system will behave like a single charge with charge 4uC
and its position is the same as the "centre of Charge" of this system which is at
10/(1+3) = 2.5 cm from the charge q1 hence the asymptote s of all field lines will amanate from this point,, hence the distance AC is 2.5 cm
such a simple and beautiful question
NOTE: I didn't have a punctilious method to solve this problem, as it proved to be too messy. So, I came up with this kind of logical solution. I don't think this is the proper way to solve it, but anyway.
Above, I have shown 2 vector addition diagrams, in which, one of the vectors is varied in magnitude. Keeping this picture in mind, let us go through a thought process.
If E 1 , E 2 represent the Electric Field due to q 1 , q 2 at a general point which lies on the path traced by the field in the problem.
∙ If q 1 grows in magnitude, E 1 will grow proportionally, and the resultant Electric field will become more steeper (taking reference from the first image).
Thus, if the line becomes more steeper, note that the length B C will also grow proportionally .
∙ If q 2 grows in magnitude, E 2 will grow proportionally, and the resultant Electric field will become less steeper (taking reference from the first image).
Thus, if the line becomes less steeper, note that the length A C will also grow proportionally .
Thus, if we let A C = ℓ , then clearly B C = 1 0 − ℓ , then,
the mathematical translations of the two points given above are,
q 1 ∝ ( 1 0 − ℓ ) and
q 2 ∝ ℓ
Dividing these two relations,
q 1 q 2 = 1 0 − ℓ ℓ
Substituting the values of q 1 and q 2 , we get,
ℓ = 2 . 5 c m
Hence,
A C = 2 . 5 c m
I even don't know if this is the correct way to arrive at the solution. I just thought that there must be some simpler way to solve this problem. So, I thought about this, I applied it, and it worked. I worked hard on the images and the typing, so please be nice in the comments even if you don't feel that this solution is correct.