Atmospheric physics 12: Solar constant

Classical Mechanics Level 2

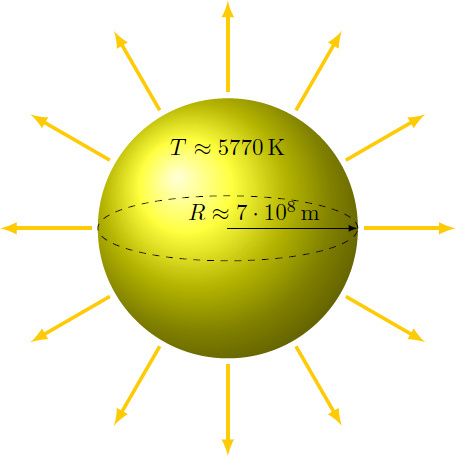
What is the radiation intensity $S_0$ of the sun, that hits the earth perpendicular to the beam direction?

This so-called solar constant $S_0$ corresponds to the maximum possible irradiation on earth's surface, when the sun is at its zenith and absorption and scattering by the earth's atmosphere can be neglected. The radiation of the sun corresponds to its thermal radiation and is emitted homogeneously in all spatial directions. The radiation intensity corresponds to energy per unit of time and per area.

Details:

The sun has the shape of a sphere with the radius $R \approx 7 \cdot 10^8 \,\text{m}$ .
The surface temperature of the sun is $T \approx 5770\,\text{K}$ .
The sun is an ideal black body, whose thermal radiation intensity at its surface is given by the Stefan Boltzmann law $I = \sigma T^4$ with $\sigma \approx 5.67 \cdot 10^{-8} \,\text{W}/\text{m}^2/\text{K}^4$ .
The distance between earth and sun is $a \approx 1.5 \cdot 10^{11} \,\text{m}$ .

S_0 \approx 86 \,\text{W}/\text{m}^2

S_0 \approx 1370 \,\text{W}/\text{m}^2

S_0 \approx 5475 \,\text{W}/\text{m}^2

S_0 \approx 342 \,\text{W}/\text{m}^2

1 solution

Markus Michelmann
Mar 8, 2018

The total power $P$ of the sun is given by the radiation intensity $I$ multiplied by its surface $A = 4\pi R^2$ : $P = I \cdot A = \sigma T^4 \cdot 4\pi R^2 \approx 3.87 \cdot 10^{26} \,\text{W}$ At a distance $a$ from the sun, the total radiation is distributed evenly on the spherical surface $A' = 4 \pi a^2$ , so that the radiation intensity results to $S_0 = \frac{P}{A'} = \sigma T^4 \left(\frac{R}{a}\right)^2 \approx 1370 \, \text{W}/\text{m}^2$

@Markus Michelmann Sir hii. How are you??I have seen your many problems in brilliant.They are awesome. Suggest me good books for Thermodynamics. Please sir can you??

A Former Brilliant Member - 1 year, 9 months ago

Atmospheric physics 12: Solar constant

1 solution

0 pending reports