Atmospheric physics 13: Earth's energy budget
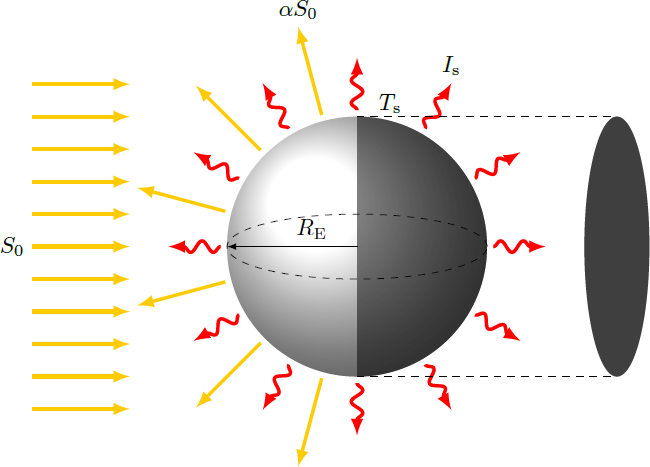
In the last problem we have determined the radiation intensity of the sun, that hits the earth (the so-called solar constant). Now suppose, that the earth's surface assumes a temperature and thus emits thermal radiation itself. Which equilibrium temperature does the earth have in this case?
Assumptions:
- The sun is at a great distance from the earth, so that the incident rays are parallel.
- The Earth's surface has an albedo of , so that 30% of the incoming sun's rays are directly reflected and do not contribute to the Earth's temperature.
- The earth has a constant and homogeneous temperature in equilibrium. For the sake of simplicity, we assume, that the polar regions and tropics of the earth are equally warm and that there is no temperature difference between the day and the night side.
- The earth's surface acts as an ideal blackbody in the infrared range, so we are allowed to use the Stefan-Boltzmann law for the thermal radiation.
- The influence of the atmosphere is neglected.
Hints: The calculation of the incident energy flow is simplified when looking at the shadow that the earth throws. (The earth's shadow corresponds to the absorbed and reflected sunbeams.)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The earth has a cross-sectional area of A = π R E 2 , so that all rays incident on this surface are absorbed or reflected. (This cross-sectional area also equal to the earth's shadow.) Thus, the incident sunlight corresponds to the total power P in = π R E 2 S 0 Reflected light and thermal radiation are emitted from the earth. The reflected light corresponds to an power P r = α P in , with the albedo α of the earth's surface. Thermal radiation is emitted from the whole surface S = 4 π R E 2 of the earth. Therefore, the outgoing energy flows results P r P th = α π R E 2 S 0 = 4 π R E 2 σ T s 4 In equilibrium, incoming and outgoing flows must be the same ⇒ ⇒ P in 4 S 0 T s = P r + P th = α 4 S 0 + σ T s 4 = [ 4 σ ( 1 − α ) S 0 ] 1 / 4 = [ 4 ⋅ 5 . 6 7 ⋅ 1 0 − 8 ( 1 − 0 . 3 ) ⋅ 1 3 7 0 ] 1 / 4 K ≈ 2 5 5 K ≈ − 1 8 ∘ C Note: Due to the spherical shape of the earth, each square meter of the surface receives on average I in = 4 1 S 0 as irradiance or I in − I r = 4 1 ( 1 − α ) S 0 a net solar intensity. The factor 4 1 reflects the ratio of cross section to the surface