Atmospheric physics 14: Greenhouse effect
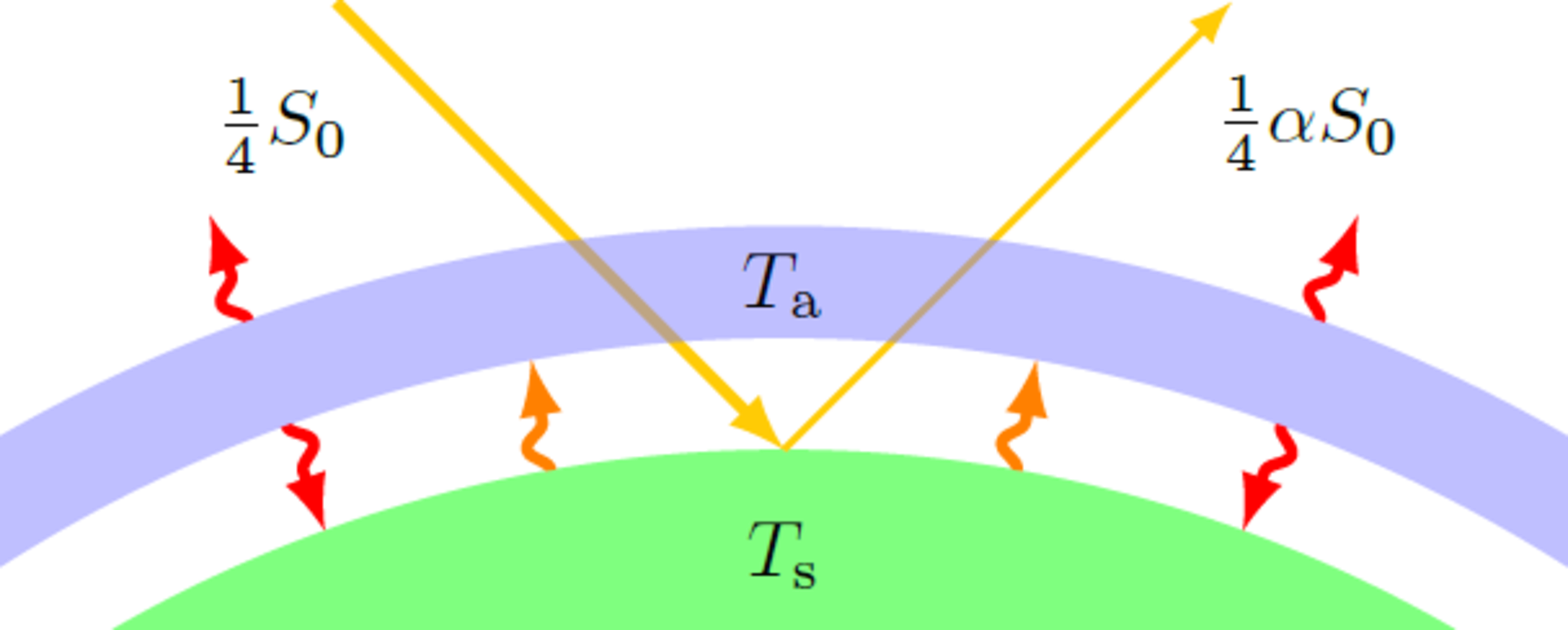
Now, considering the radiation balance of the earth, we also want to include the atmosphere. We assume that the atmosphere is transparent to sunlight, but completely absorbs the thermal infrared radiation of the earth. What value then results for the surface temperature of the earth?
Assumptions:
- The earth's surface has an albedo of .
- The atmosphere and surface have homogeneous temperatures and , respectively.
- The atmosphere gives off heat radiation into space and onto the earth's surface with equal intensity.
- Both the atmosphere and the surface are considered to be perfect black bodies in the infrared range.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the solar radiation, we must take into account the factor 4 1 in the intensity, since only a part of the earth is illuminated at a time, and we consider the average solar irradiance over the entire earth's surface. (For details, see the previous problem.) The corresponding energy flows thus result I in = 4 1 S 0 and I r = 4 1 ( 1 − α ) S 0 .
For the energy balance of earth and atmosphere, we must set up two equations, each corresponding to the transport space-atmosphere and atmosphere-surface. Downward (positive) flows are on the left side and upwards (negative) flows are the right side of the equation: I in I in + I a = I r + I a = I r + I s (space-atmosphere) (atmosphere-surface) Here, I a = σ T a 4 and I s = σ T s 4 respectively denote the thermal radiation of atmosphere and surface. In the second equation, I a appears as a source term, because the thermal radiation of the atmosphere causes additional heating of the earth's surface. We can rewrite the equations as follows 4 1 − α S 0 4 1 − α S 0 + σ T a 4 = σ T a 4 = σ T s 4 ⇒ T a ⇒ T s = [ 4 σ ( 1 − α ) S 0 ] 1 / 4 = [ 2 σ ( 1 − α ) S 0 ] 1 / 4 = 2 1 / 4 T a While the temperature of the atmosphere corresponds to the value T a = 2 5 5 K , we determined in the last problem, the temperature of the surface is larger by a factor 2 1 / 4 , so that T s = [ 2 ⋅ 5 . 6 7 ⋅ 1 0 − 8 ( 1 − 0 . 3 ) 1 3 7 0 ] 1 / 4 K ≈ 1 . 1 8 9 ⋅ 2 5 5 K ≈ 3 0 3 K ≈ + 3 0 ∘ C