Atmospheric physics 15: Emissivity of the atmosphere

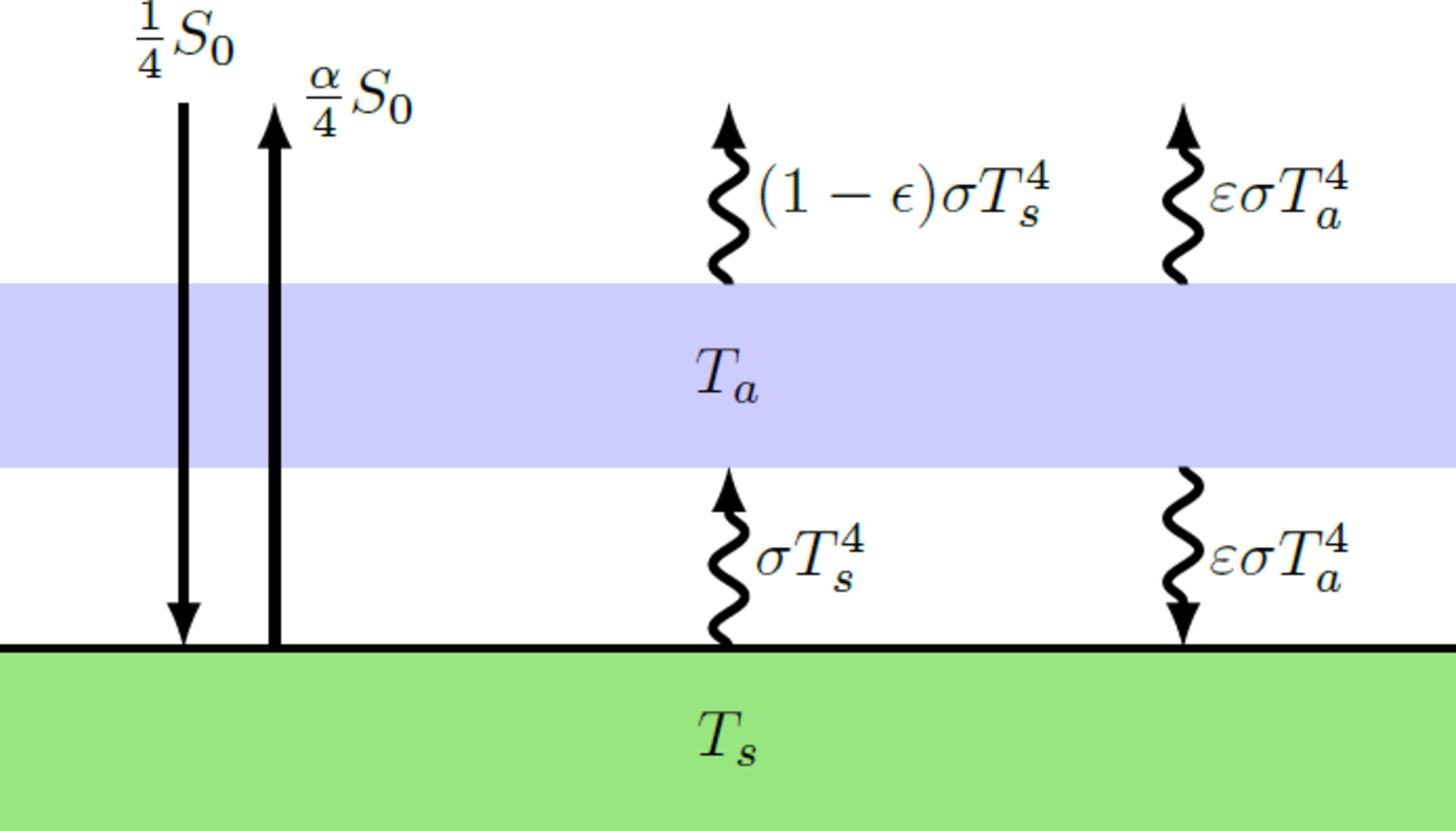
Classical Mechanics Level pending

The assumption, that the atmosphere completely absorbs the heat radiation of the earth, leads to a much stronger greenhouse effect, than we observe in reality. In fact, there are several windows in the absorption spectrum of the atmosphere, so that only a part of the thermal radiation is absorbed. For a more realistic model of the greenhouse effect, it is therefore assumed, that there is a gray atmosphere, that has an emissivity ε < 1 \varepsilon < 1 .

What is the value of the emissivity ε \varepsilon of earth's atmosphere, so that the surface temperature is equal to the actual mean temperature T s = 288 K T_\text{s} = 288 \,\text{K} ?

Details and Assumptions:

  • The emissivity ε \varepsilon indicates the proportion of the incident radiation, that is absorbed by the atmosphere. Thus, the earth's surface emits the intensity ( 1 − ε ) σ T s 4 (1 - \varepsilon) \sigma T_\text{s}^4 directly into space, while the part ε σ T s 4 \varepsilon \sigma T_\text{s}^4 is absorped.
  • The emissivity ε \varepsilon also describes the thermal radiation efficiency of the atmosphere. Thus, the atmosphere radiates the intensity ε σ T a 4 \varepsilon \sigma T_\text{a}^4 as heat radiation into space and onto earth's surface.
  • For the sunlight, the atmosphere is still transparent, while the earth's surface has an albedo α = 0.3 \alpha = 0.3 for visible light.
ε ≈ 0.53 \varepsilon \approx 0.53 ε ≈ 0.86 \varepsilon \approx 0.86 ε ≈ 0.14 \varepsilon \approx 0.14 ε ≈ 0.38 \varepsilon \approx 0.38 ε ≈ 0.77 \varepsilon \approx 0.77

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

In contrast to the last problem, the radiation of the atmosphere must be modified to I a = ε σ T a 4 I_\text{a} = \varepsilon \sigma T_\text{a}^4 . In addition, we get the transmission I t,s = ( 1 − ε ) σ T s 4 I_\text{t,s} = (1 -\varepsilon) \sigma T_\text{s}^4 through the atmosphere as another term. The energy balance is therefore I in = I r + I t,s + I a I in + I a = I r + I s \begin{aligned} I_\text{in} &= I_\text{r} + I_\text{t,s} + I_\text{a} \\ I_\text{in} + I_\text{a} &= I_\text{r} + I_\text{s} \end{aligned} This equations can be rewritten to 1 − α 4 S 0 = ( 1 − ε ) σ T s 4 + ε σ T a 4 1 − α 4 S 0 = σ T s 4 − ε σ T a 4 \begin{aligned} \frac{1-\alpha}{4} S_0 &= (1- \varepsilon) \sigma T_\text{s}^4 + \varepsilon \sigma T_\text{a}^4 \\ \frac{1-\alpha}{4} S_0 &= \sigma T_\text{s}^4 - \varepsilon \sigma T_\text{a}^4 \end{aligned} Thus we obtain a linear system of equations for the two unknowns T s 4 T_\text{s}^4 and T a 4 T_\text{a}^4 , that can be solved by matrix inversion: [ 1 − ε ε 1 − ε ] [ T s 4 T a 4 ] = ( 1 − α ) S 0 4 σ [ 1 1 ] ⇒ [ T s 4 T a 4 ] = ( 1 − α ) S 0 4 σ 1 ε ( 2 − ε ) [ ε ε 1 − ( 1 − ε ) ] [ 1 1 ] = ( 1 − α ) S 0 4 ( 2 − ε ) σ [ 2 1 ] \begin{aligned} \left[ \begin{array}{cc} 1 - \varepsilon & \varepsilon \\ 1 & - \varepsilon \end{array} \right] \left[ \begin{array}{c} T_\text{s}^4 \\ T_\text{a}^4 \end{array} \right] &= \frac{(1- \alpha) S_0}{4 \sigma} \left[ \begin{array}{c} 1 \\ 1 \end{array}\right] \\ \Rightarrow \qquad \left[ \begin{array}{c} T_\text{s}^4 \\ T_\text{a}^4 \end{array} \right] &= \frac{(1- \alpha) S_0}{4 \sigma} \frac{1}{\varepsilon (2 - \varepsilon)} \left[ \begin{array}{cc} \varepsilon & \varepsilon \\ 1 & -(1- \varepsilon) \end{array} \right] \left[ \begin{array}{c} 1 \\ 1 \end{array}\right] \\ &= \frac{(1- \alpha) S_0}{4 (2 - \varepsilon) \sigma} \left[ \begin{array}{c} 2 \\ 1 \end{array}\right] \end{aligned} For the surface temperature therefore applies T s = [ 1 2 − ε ( 1 − α ) S 0 2 σ ] 1 / 4 = { [ ( 1 − α ) S 0 4 σ ] 1 / 4 ≈ 255 K ε = 0 [ ( 1 − α ) S 0 2 σ ] 1 / 4 ≈ 303 K ε = 1 T_\text{s} = \left[ \frac{1}{2 - \varepsilon} \frac{(1 - \alpha) S_0}{2 \sigma} \right]^{1/4} = \begin{cases} \left[ \frac{(1 - \alpha) S_0}{4 \sigma} \right]^{1/4} \approx 255\,\text{K} & \varepsilon = 0 \\ \left[ \frac{(1 - \alpha) S_0}{2 \sigma} \right]^{1/4} \approx 303\,\text{K} & \varepsilon = 1 \end{cases} The solution contains the two preceding solutions as special cases for ε = 0 \varepsilon = 0 and ε = 1 \varepsilon = 1 . If the general equation is solved for the emissivity, the result is ε = 2 − ( 1 − α ) S 0 2 σ T s 4 = 2 − ( 1 − 0.3 ) ⋅ 1370 2 ⋅ 5.67 ⋅ 1 0 − 8 ⋅ 28 8 4 ≈ 0.77 \varepsilon = 2 - \frac{(1 - \alpha) S_0}{2 \sigma T_\text{s}^4} = 2 - \frac{(1 - 0.3) \cdot 1370 }{2 \cdot 5.67 \cdot 10^{-8} \cdot 288^4} \approx 0.77

0 Helpful 1 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...