Atmospheric physics 8: Buoyancy acceleration

Classical Mechanics Level 2

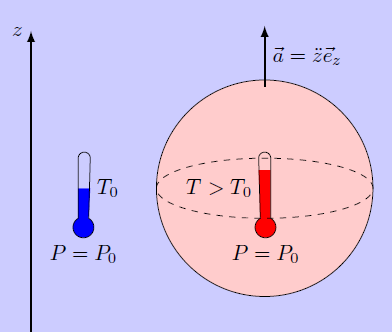
In the atmosphere with the temperature T 0 = 288 K T_0 = 288\,\text{K} there is a warmer air parcel with a temperature T = 291 K T = 291 \,\text{K} . How large is the acceleration a a of this air parcel in vertical direction due to buoyancy and gravity? (The density of gases decreases with temperature, so that warm air is lighter than cold air. Thus, warm air rises in the atmosphere as it experiences a positive net buoyancy force in the cooler ambient air.)

Assumptions:

  • Air is an ideal gas and follows the general gas equation P = R ∗ ρ T P = R^\ast \rho T .
  • The pressure of the air parcel and the surrounding atmosphere is the same ( P = P 0 P = P_0 ).
  • Air resistance is neglected.
a ≈ 10 m / s 2 a \approx 10 \,\text{m}/\text{s}^2 a ≈ 0.01 m / s 2 a \approx 0.01 \,\text{m}/\text{s}^2 a ≈ 0.1 m / s 2 a \approx 0.1 \,\text{m}/\text{s}^2 a ≈ 1 m / s 2 a \approx 1 \,\text{m}/\text{s}^2

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

According to the Archimedean principle, the buoyancy force F b = + m 0 g F_b = + m_0 g corresponds to the weight of the displaced air of mass m 0 = ρ 0 V m_0 = \rho_0 V , where V V is the volume of the air parcel. The air parcel of mass m = ρ V m = \rho V also experiences a gravitational force F g = − m g F_g = - m g . The sum of both forces is according to Newton equal to the inertial force m a = F b + F g = ( m 0 − m ) g ⇒ a = m 0 − m m g = ρ 0 − ρ ρ g = 1 / T 0 − 1 / T 1 / T g = T 0 − T T 0 g \begin{aligned} & & m a &= F_b + F_g = (m_0 - m) g \\ \Rightarrow & & a &= \frac{m_0 - m}{m} g \\ & & &= \frac{\rho_0 - \rho}{\rho} g \\ & & &= \frac{1/T_0 - 1/T}{1/T} g \\ & & &= \frac{T_0 - T}{T_0} g \end{aligned} Here we used the fact, that according to the ideal gas law the density at constant pressure is inversely proportional to the temperature ( ρ ∝ 1 / T \rho \propto 1/T ). If we plug numbers into the equation, we get the final result a = 291 K − 288 K 291 K ⋅ 9.81 m / s 2 ≈ 0.1 m / s 2 a = \frac{291\,\text{K} - 288 \,\text{K}}{291 \,\text{K}} \cdot 9.81 \,\text{m}/\text{s}^2 \approx 0.1 \,\text{m}/\text{s}^2

0 Helpful 0 Interesting 0 Brilliant 0 Confused

ok a bit of 'handwaving' : the parcel has a 1% higher temperature than it's surrounding (+3 K to 300 K) so about 1% less density so it experiences a buoyancy forse of about 1% of the gravitational acceleration g = 10 m/s^2 , which gives the answer.

Of course the question really is: because of 'friction' what will its steady (final) velocity be?

I honestly don't know the answer, although I suspect it reaches it very quickly. Cheers ! :-)

Theo-wpm Hermsen - 3 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...