Can you drop a circle on a segment ?
Two segments, no matter their respective lengths, have the same "number" of points on them. There are several ways to see it geometrically.
Here is one possible construction:
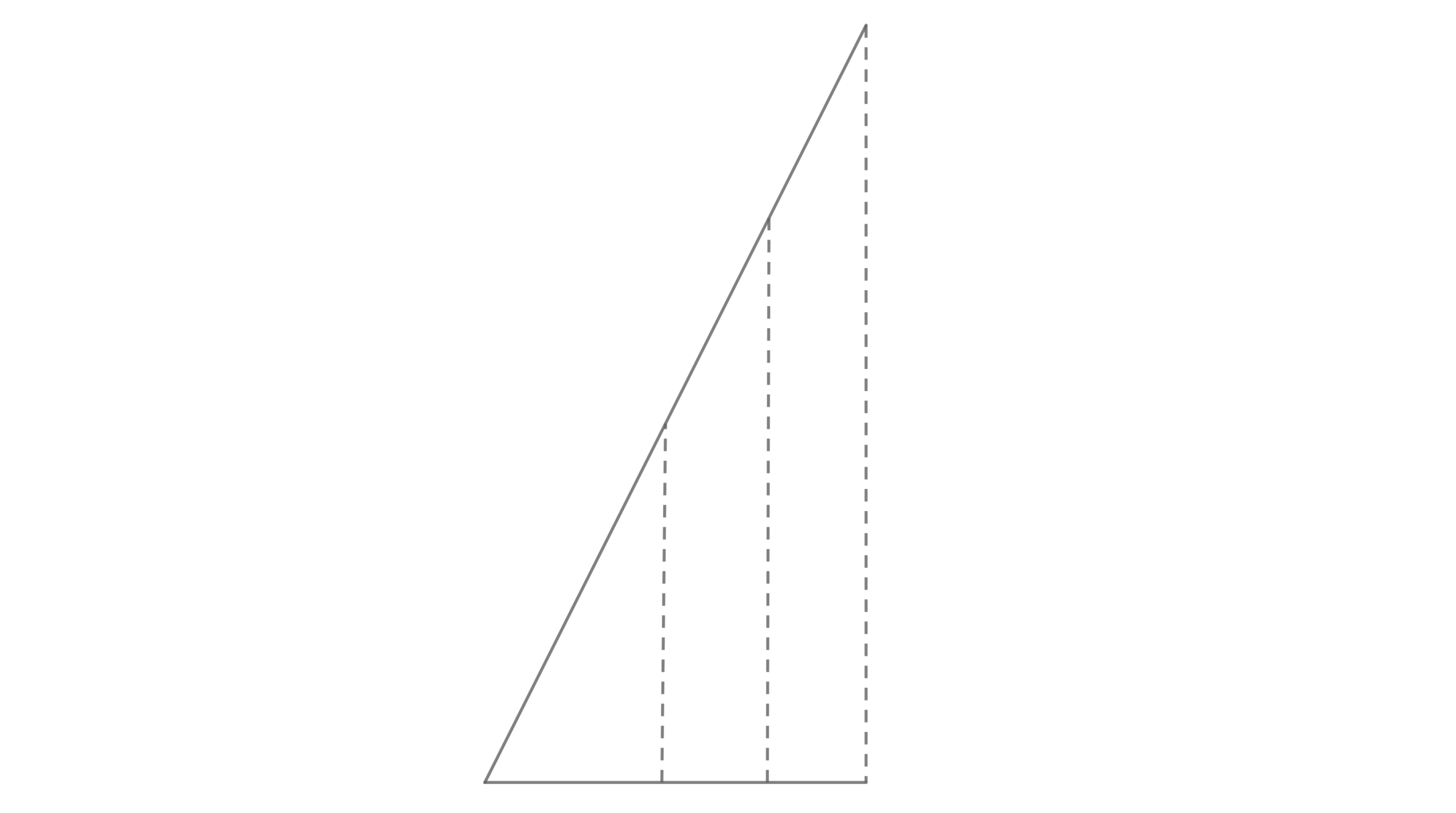
Basically, if you connect the two segments such that they form a right triangle, then using orthogonal projection (meaning you "drop" the point from a segment to another) we can see every point from segment A matches with a different point from segment B and vice versa.
It's also true that a circle and a line segment have the same "number" of points. But is there any way to see it geometrically?
A.
Yes, there is.
B.
Yes, there is, but finding it is still an open problem.
C.
No there isn't, because of stuff related to constructible numbers.
D.
No there isn't, because of other stuff.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
NB : I insisted on the "seeing" part because demonstrating the validity of such a construction requires the Cantor-Bernstein theorem and the goal of the problem is just the intuition.