Auxiliary Line Problem

Insight: $\Delta ABC$ and $\Delta ADC$ can be pieced together to form an equilateral triangle.

$1. \angle BAC = \angle CAD \implies BC = DC$ (equal chords subtend equal inscribed angle)

$2.$ Construct $\Delta EBC$ which is congruent to $\Delta ADC$

$3. \angle ABC + \angle ADC = 180^{\circ} \implies \angle ABC + \angle EBC = 180^{\circ} \implies ABE \text{ are collinear}$

$4. BE = AD = 45, AE = 32+45 = 77$

$5. \angle BEC = \angle DAC = 60^{\circ} \implies \Delta ACE \text{ is equilateral} \implies AE = x$

$\therefore x = 77$

We have $\Delta CBD$ is equilateral. $\therefore$ By special case of Ptolemy's theorem, $x = AC = AB+BD =32 +45 =77$

Define y = <ADC. Then <ABC = 180 - y since they are inscribed angles whose arcs add to 360. Then <ACD = 120 - y, and < ACB = y - 60. In triangle BCD, we have by the Law of sines, x//sin(y) = 45/sin(120 -y). In triangle ABC, we have x/sin(180 - y) = x/sin(y) =32/sin(y - 60). Therefore, 45/sin(120 - y) = 32/sin(y - 60). Cross-multiplying, and expanding the sine functions leads to the following equation: 77 sqrt(3) cos(y) = 13*sin(y). Squaring both sides, and substituting yields: cos(y) = 13/134, so y = 84.43269763.. Substitution in either of the first two equations gives x =77. Ed Gray

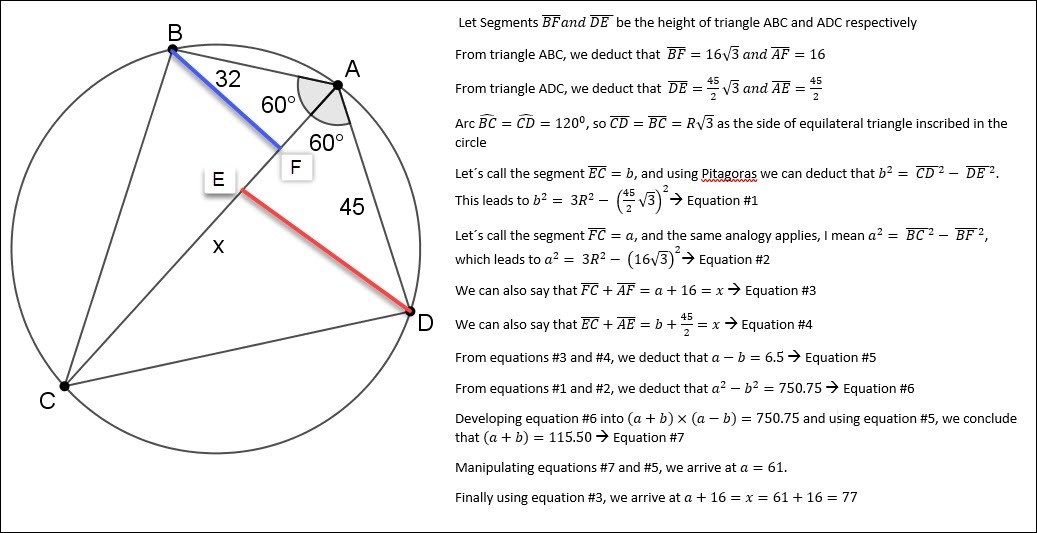
No need to mention that my solution is a bit more complicated than the others presented here.

Let <ACD = a, then using sin rule for ΔABC, and ΔACD repectively, 32/sin(60 – a) = x/ sin(60 + a) , and 45/sin (a) = x/sin(120 – a). From the first equations we get, tan (a) = √3(x – 32)/(x + 32), and from the second eqs., we get, tan (a) = 45√3/(2x – 45), and we can find x from substitution,
45 x – 45(32) = 2x^2 – 109 x +45(32), then x^2 – 77 x=0, x=77