Average area bound by tangent lines
This problem is a follow up of a problem I made previously. Take a look at the following pictures.
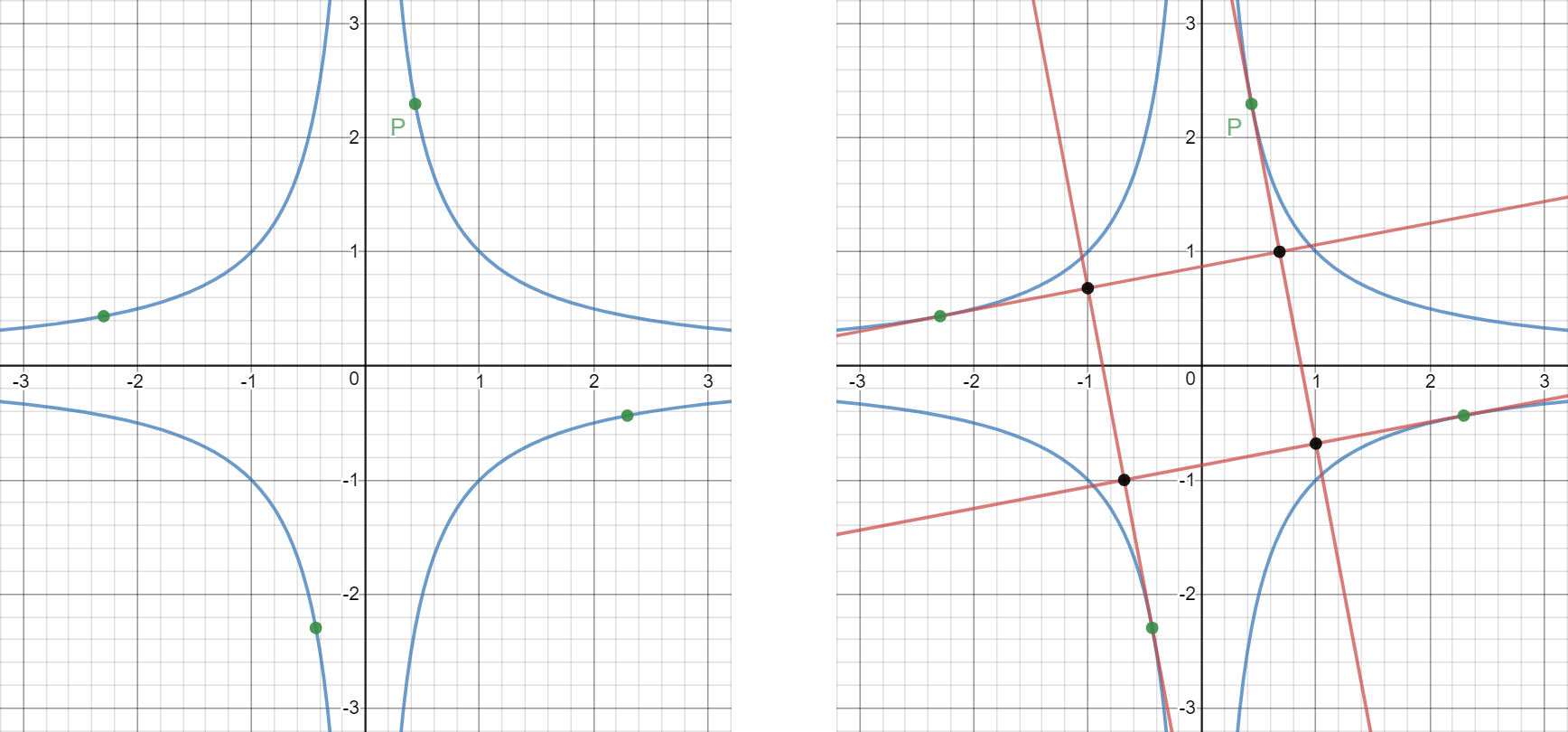 In those pictures you can see the graph of the curve
. Let
be a random point on the graph in the first quadrant, such that
.
Also mark the three points
rotated around the origin by
,
and
respectively. Now draw tangent lines to the curve at those four points. The tangent lines will intersect two other tangent lines, as seen in the right picture above. Let
be the area enclosed by those four tangent lines. If we vary
, you will notice that
will be different in size. Let
be the average of
on the interval
, then
can be given by
where
, such that
and
are prime. Find
.
In those pictures you can see the graph of the curve
. Let
be a random point on the graph in the first quadrant, such that
.
Also mark the three points
rotated around the origin by
,
and
respectively. Now draw tangent lines to the curve at those four points. The tangent lines will intersect two other tangent lines, as seen in the right picture above. Let
be the area enclosed by those four tangent lines. If we vary
, you will notice that
will be different in size. Let
be the average of
on the interval
, then
can be given by
where
, such that
and
are prime. Find
.
Note: For all , .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We start by finding a formula for the tangent line, say l , to the curve through P . Using our knowledge about tangent lines, we find that l : y = − p 2 x + p 2 . By symmetry in each quadrant (rotating the first quadrant about 90 degrees will give you the second quadrant for example), we see that tangent lines to the curve to the rotated points will be either parallel, or perpendicular to the tangent line. If we were to search for the tangent line, say k , to the point P rotated around the origin by π / 2 radians, then we will end up with k : y = p 2 ⋅ x + 2 p . We now want to find the intersection between those two tangent lines. Solving the system of equations containing the lines l and k results in the point Q ( − 2 ⋅ p 4 + 1 p 3 − p , 2 ⋅ p 4 + 1 p 3 + p ) . What we need to know is the length of the linesegment from O to Q (O here is the origin). We find that d ( O , Q ) = 4 ⋅ ( p 4 + 1 ) 2 ( p 3 − p ) 2 + ( p 3 + p ) 2 = p 4 + 1 2 2 ( p 6 − p 2 ) = p 4 + 1 2 p 2 . If we look at the right picture, we will see that A ( p ) = 2 ( d ( O , Q ) ) 2 = p 4 + 1 1 6 p 2 . We want to find A = 1 − 0 1 ∫ 0 1 A ( p ) d p = 1 6 ⋅ ∫ 0 1 p 4 + 1 p 2 d p . Solving this integral requires some work. We can factor p 4 + 1 by p 2 + p 2 + 1 and p 2 − p 2 + 1 , after which we apply partial fractions decomposition. I = ∫ 0 1 p 4 + 1 p 2 d p = ∫ 0 1 ( p 2 + p 2 + 1 ) ( p 2 − p 2 + 1 ) p 2 d p = ∫ 0 1 2 2 ( p 2 − p 2 + 1 ) p − 2 2 ( p 2 + p 2 + 1 ) p d p ⟹ I = ∫ 0 1 4 2 ( p 2 − p 2 + 1 ) 2 p − 2 + 2 − 4 2 ( p 2 + p 2 + 1 ) 2 p + 2 − 2 d p = 4 2 1 ln ( p 2 + p 2 + 1 p 2 − p 2 + 1 ) ∣ ∣ ∣ ∣ ∣ 0 1 + ∫ 0 1 4 2 ( p 2 − p 2 + 1 ) 2 + 4 2 ( p 2 + p 2 + 1 ) 2 d p ⟹ I = 4 2 1 ln ( 2 + 2 2 − 2 ) + 4 1 ∫ 0 1 p 2 − p 2 + 1 1 + p 2 + p 2 + 1 1 d p = 4 2 1 ln ( 2 6 − 4 2 ) + 4 1 ∫ 0 1 ( p − 2 1 ) 2 + 2 1 1 d p + 4 1 ∫ 0 1 ( p + 2 1 ) 2 + 2 1 1 d p . Substitute p = 2 u + 1 in the left integrand and p = 2 v − 1 in the right integrand, then d p = d u / 2 and d p = d v / 2 . So I = 4 2 1 ln ( 3 − 2 2 ) + 4 1 ∫ u ( 0 ) u ( 1 ) u 2 + 1 2 d u + 4 1 ∫ v ( 0 ) v ( 1 ) v 2 + 1 2 d v = 4 2 1 ln ( 3 − 2 2 ) + 2 2 1 arctan ( p 2 − 1 ) ∣ ∣ ∣ ∣ 0 1 + 2 2 1 arctan ( p 2 + 1 ) ∣ ∣ ∣ ∣ 0 1 ⟹ I = 4 2 1 ln ( 3 − 2 2 ) + 2 2 1 ( arctan ( 2 − 1 ) − arctan ( − 1 ) + arctan ( 1 + 2 ) − arctan ( 1 ) ) . Notice that 2 − 1 1 = 2 + 1 , so arctan ( 2 + 1 ) + arctan ( 2 − 1 ) = π / 2 . Furthermore, arctan ( ⋅ ) is an odd function, so we see that I = 4 2 1 ln ( 3 − 2 2 ) + 4 2 π . We can now conclude that A = 1 6 ⋅ 4 2 1 ln ( 3 − 2 2 ) + 4 2 π = 2 2 ( π + ln ( 3 − 2 2 ) ) , and thus a + b + c + d + e = 2 + 2 + 3 − 2 + 2 = 7 .