Average Distance Between Two Points

By calculating the pdf of many random variables it is tedious but not difficult to show that the answer is given by: $\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\sqrt{(x-y)^2+(z-w)^2}dx\, dy\, dz\, dw = \frac{1}{15}\left(2+\sqrt{2}+5\log(1+\sqrt{2})\right).$

We can use a Monte Carlo Simulation , and simply randomly pick points in the square, compute their distance, and average this for many points:

Python 3.3:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

from random import random as r
from math import sqrt
from time import time
def distance(a,b,c,d):
    return sqrt(abs((a-c)**2+(b-d)**2))
total = 0
trials = 0
end = 10 + time()
while time() < end:
    total += distance(r(),r(),r(),r())
    trials += 1
print ("Answer:", total / trials)

I posted this problem under computer science because the manual method for doing this involves some pretty nasty calculus. I also put "Correct to 4 places after the decimal" so that your computers would have to crank for a good few seconds.

This can (I don't know any other way) be done rather simply by sampling tons of pseudo-random points via a Monte Carlo simulation. With that said, your pseudo-random number generating algorithm must produce uniformly distributed numbers. For my solution, I used the well known Mersenne Twister algorithm.

Pardon my c++ by the way.

Here is the header file mrand.h , and the library file mrand.cpp .

#include "mtrand.h"
#include <cmath>
#include <ctime>
#include <stdio.h>

struct point{    //to help with readability
    point(double X, double Y):x(X),y(Y){};
    double x;
    double y;
};

double square(double x){   //I don't like the standard pow(X,n) function
    return x*x;
}

double distance(const point& a, const point& b){  //calculate and return the distance between a & b
    double Y = b.y - a.y;
    double X = b.x - a.x;
    return (sqrt((square(Y)) + (square(X))));
}

int main() {
    int seed = time(NULL);  //set random seed
    MTRand rand_num(seed);  //initialize generator
    double Box_X = 1.;      //box width
    double Box_Y = 1.;      //box height

    double expected_dist = 0;   //start off the expected distance

    int N = 2000000;            //number of samples
    double N_inv = 1. / ((double)N);  //multiplication is faster than division

    point A(0,0);  //initialize the points we'll be manipulating
    point B(0,0);
    for (int i=1; i<N; ++i){
        A = point(rand_num(),rand_num());
        B = point(rand_num(),rand_num());
        expected_dist+=distance(A,B);  //sum the distances
    }

    expected_dist*=N_inv;   //get the average

    printf("The expected distance is : %.9fl ",expected_dist);  //print result

    return 0;
}

In Python: import random import math

def dist(a, b):
    dx = a[0] - b[0]
    dy = a[1] - b[1]
    return math.sqrt(dx*dx + dy*dy)

total = 0
count = 0
while True:
    a = (random.random(), random.random())
    b = (random.random(), random.random())
    total += dist(a, b)
    count += 1

    # print progress, visually inspect and guess when it has converged
    if (count % 100000) == 0:
        print float(total)/count

The module of a generic $\vec{r}$ vector is given by:

$r = \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2}$

So all we have to do is generate the pairs of coordinates like $(x_0,y_0)$ , $(x_1,y_1)$ randomly in the interval $[1,1]$ and calculate the mean of many $r$ . Using the Monte Carlo Method we easily note that the larger the sample size, the more accurate the result are (see the code below). But, how big should the sample be to get an accurate answer? Well, it is difficult to determine the error without knowing the exact value. In this case, we generally use statistical inference (see chapter 2 of this book ). So, to give a more adequate answer the code here calculates not only the average but the error with the confidence coefficient.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

#include<iostream>    // std::cout
#include<stdlib.h>      // srand
#include<time.h>  // time
#include<vector>  // std::vector
#include<math.h>  // pow

// return values between min and max
double randomDouble(double min, double max);

// fill a vector with coordenates (x0, x1), (y0, y1)
void fillVector(std::vector<double> &v);

int main(){

    srand(time(NULL));

    std::vector<double> v;
    double sum = 0.0;
    double mean = 0.0;
    double deltaX = 0.0;
    double deltaY = 0.0;
    int sampleSize = 1E8; // sample size

    for(int n = 0; n < sampleSize; n++){
        fillVector(v);
        deltaX = v.at(1) - v.at(0);
        deltaY = v.at(3) - v.at(2);

        sum += sqrt(pow(deltaX, 2) + pow(deltaY, 2));
    }

    mean = sum / double(sampleSize);
    std::cout << "The expected value provide by Monte Carlo Method with " << sampleSize
              << " variables is: " << mean << std::endl;
    return 0;
}

double randomDouble(double min, double max){
    return (max - min) * ((double)rand() / (double)RAND_MAX) + min;
}

void fillVector(std::vector<double> &v){
    v.clear();
    for(int i = 0; i < 4; i++){
        v.push_back(randomDouble(0.0, 1.0));    
    }
}

// Typical output:
// The expected value provide by Monte Carlo Method with 100000000 variables is: 0.521443

Monte Carlo Simulation: randomly pick two points in the square, compute their distance. Then try trails for many times, calculate the sum of all distances, and get the average value. Here is my code solution to 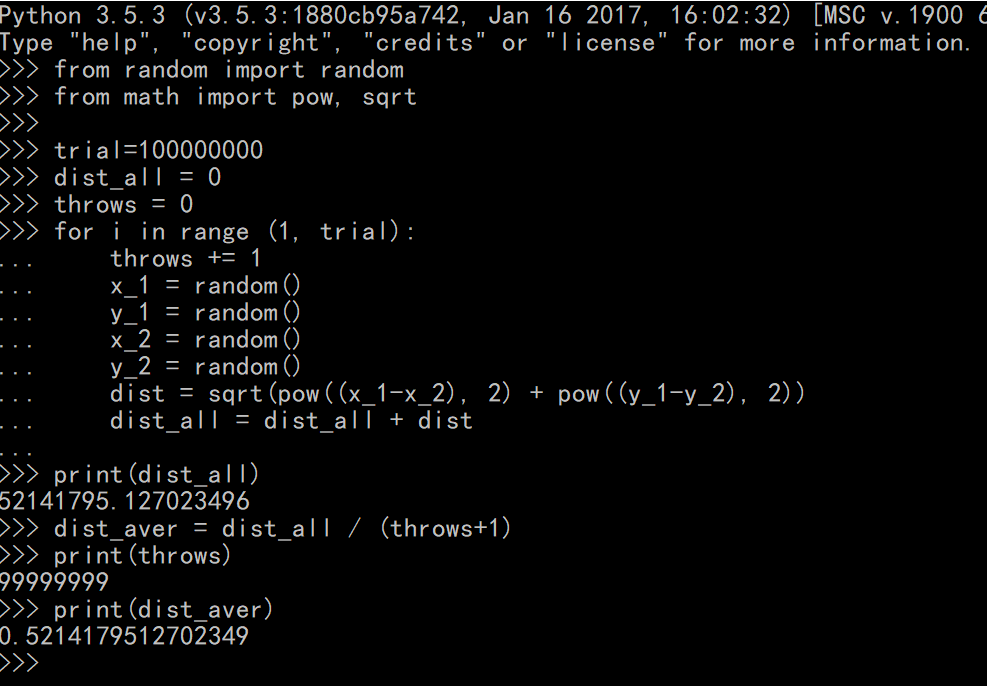this question.

Solution using complex numbers:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

from random import random

def MonteCarlo(numTrials):
  sumDistances = 0.0

  for trial in xrange(numTrials):
    point1 = complex(random(), random())
    point2 = complex(random(), random())
    sumDistances += abs(point2 - point1)

  return sumDistances/numTrials

print MonteCarlo(10**6) #Answer: ~0.5210

This is my Python3 code:

import random, math

def randomfunc():

i = 1

while i <= 100000:

    x1 = random.uniform(0,1)

    y1 = random.uniform(0,1)

    x2 = random.uniform(0,1)

    y2 = random.uniform(0,1)

    s = math.sqrt((x1-y1)**2 + (x2-y2)**2)

    yield s

    i += 1

sums = sum(list(randomfunc()))

frequen = len(list(randomfunc()))

print (sums/frequen)

printscreen(0.5210169751734656) I wonder it only use less than 10 seconds to pop up an answer, it was 100000 times of calculation!!