Average limit

Relevant wiki: Linear Recurrence Relations - With Repeated Roots

Since $A_n = \dfrac {A_{n-1}+A_{n-2}}2$ , $\implies 2 A_n = A_{n-1}+A_{n-2}$ . Therefore, the characteristic equation is as follows:

$\begin{aligned} 2r^2 -r-1 & = 0 \\ (r-1)(2r+1) & = 0 \\ \implies r & = \begin{cases} 1 \\ -\frac 12 \end{cases} \\ \implies A_n & = {\color{#3D99F6} c_1} + {\color{#3D99F6} c_2} \left(-\frac 12\right)^n & \small \color{#3D99F6} \text{where }c_1, \ c_2 \text{ are constants.} \end{aligned}$

$\begin{cases} A_0 = a & \implies c_1 + c_2 = a & ...(1) \\ A_1 = b & \implies c_1 - \dfrac {c_2}2 = b & ...(2) \end{cases}$

$(1)-(2): \quad \dfrac 32 c_2 = (a-b) \implies c_2 = \dfrac 23 (a-b)$

$(1): \quad c_1 = a - c_2 = a - \dfrac 23 (a-b) = \dfrac 13 (a+2b)$

$\begin{aligned} \implies A_n & = \frac 13 a + \frac 23 b + \frac 23 \left(-\frac 12\right)^n (a-b) \\ \lim_{n \to \infty} A_n & = \lim_{n \to \infty} \frac 13 a + \frac 23 b + \frac 23 \left(-\frac 12\right)^n (a-b) \\ & = \frac 13 a + \frac 23 b \end{aligned}$

$\implies X = 0$ , $Y=\dfrac 13$ , $Z=\dfrac 23$ , $W=0$ and $YZ+X-W = \dfrac 13 \cdot \dfrac 23 +0-0 = \dfrac 29 \approx \boxed{0.222}$

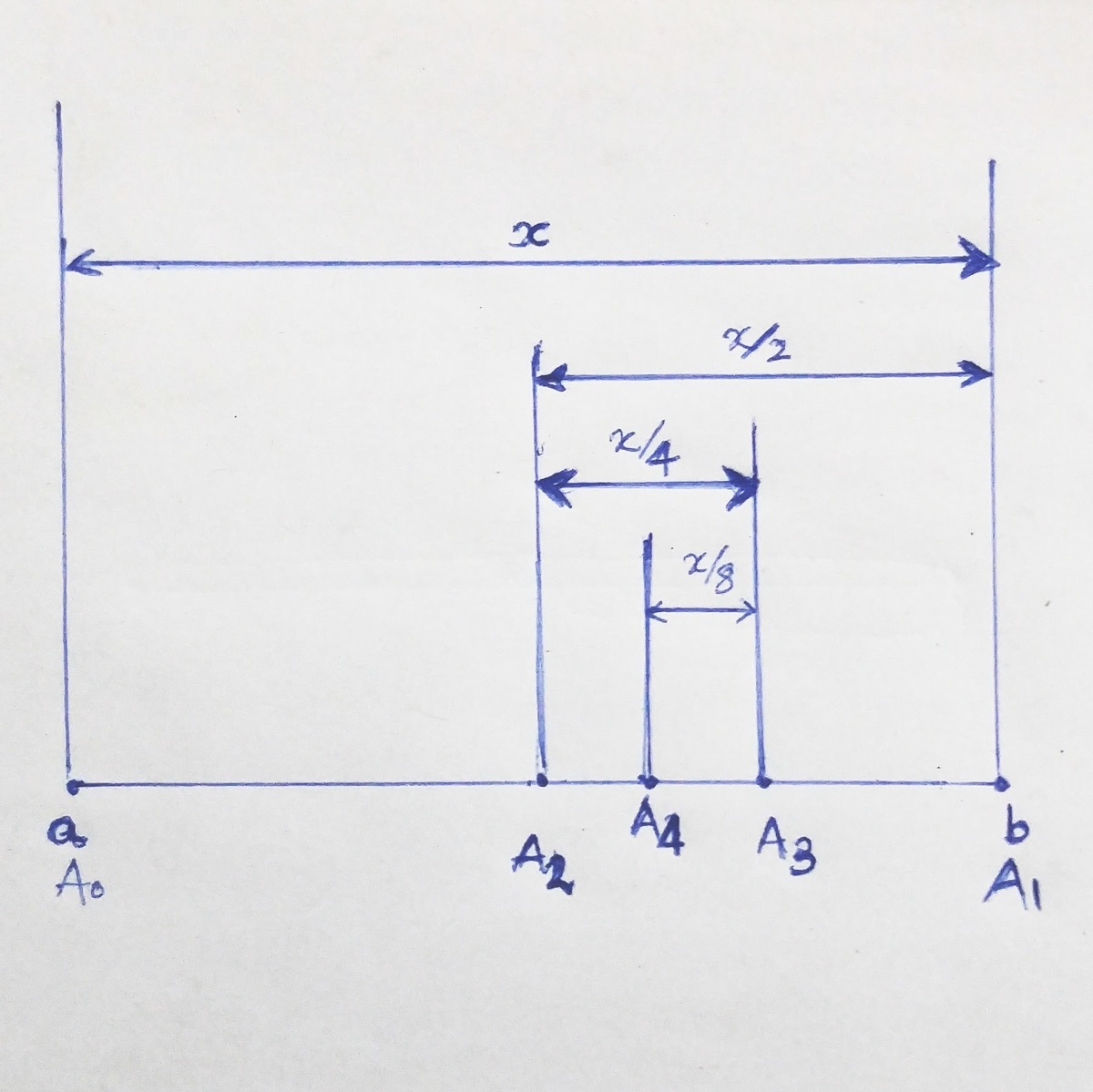
If we plot $a$ and $b$ along a number line as shown in the figure above

$\begin{aligned}A_{1}&=a+x&\small\color{#3D99F6}\text{"x" is the distance between a and b,i.e, }x=b-a\\ A_{2}&=a+(x-\dfrac{x}{2})\\ A_{3}&=a+(x-\dfrac{x}{2}+\dfrac{x}{4})\\ A_{n}&=a+x\left(\sum_{k=0}^{n-1}(\dfrac{-1}{2})^k\right)\\ \lim_{n\to\infty}A_{n}&=a+x\left(\sum_{k=0}^{\infty}(\dfrac{-1}{2})^k\right)\\ &=a+x\left(\dfrac{1}{1+\dfrac{1}{2}}\right)\\ &=a+x\left(\dfrac{2}{3}\right)=a+\dfrac{2}{3}(b-a)\\ &=\dfrac{a}{3}+\dfrac{2b}{3}\\ \text{Thus,}\\ &\color{#D61F06}\boxed{W=0},\boxed{X=0},\boxed{Y=\dfrac{1}{3}},\boxed{Z=\dfrac{2}{3}}\\&\color{#D61F06}YZ+X-W=\boxed{\dfrac{2}{9}}\end{aligned}$

Calculating $A_{-1}$ and $A_{-2}$ , to use the Z-transform :

$\large \displaystyle 2A_1 = A_0 + A_{-1}$

$\large \displaystyle 2b = a + A_{-1}$

$\color{#20A900} \boxed{\large \displaystyle A_{-1} = 2b-a}$

$\large \displaystyle 2A_0 = A_{-1} + A_{-2}$

$\large \displaystyle 2a = 2b-a + A_{-2}$

$\color{#20A900} \boxed{\large \displaystyle A_{-2} = 3a-2b}$

So, applying the Z-transform in the equation:

$\large \displaystyle 2A(z) = z^{-1} A(z) + A_{-1} + z^{-2} A(z) + z^{-1} A_{-1} + A_{-2}$

$\large \displaystyle A(z) = \frac{2a + (2b-a)z^{-1}}{2 - z^{-1} - z^{-2}}$

$\large \displaystyle A(z) = \frac{a + (b-0.5a)z^{-1}}{1 - 0.5z^{-1} - 0.5z^{-2}}$

By partial fractions:

$\large \displaystyle A(z) = \frac13 \left [ \frac{2a-2b}{1 + 0.5z^{-1}} + \frac{a+2b}{1 - z^{-1}} \right ]$

Applying inverse Z-transform:

$\color{#20A900} \boxed{ \large \displaystyle A_n = \frac13 \left [ (2a-2b)\cdot (-0.5)^n + (a+2b) \right ] }$

When $n \rightarrow \infty$ :

$\color{#20A900} \boxed{ \large \displaystyle \lim_{n \rightarrow \infty} A_n = \frac13 (a+2b) }$

So:

$\color{#3D99F6} \boxed{\large \displaystyle X = 0}, \boxed{\large \displaystyle Y = \frac13}, \boxed{\large \displaystyle Z = \frac23}, \boxed{\large \displaystyle W = 0}$ , making the answer $\color{#3D99F6} \boxed{\large \displaystyle \frac29 }$