Average Period
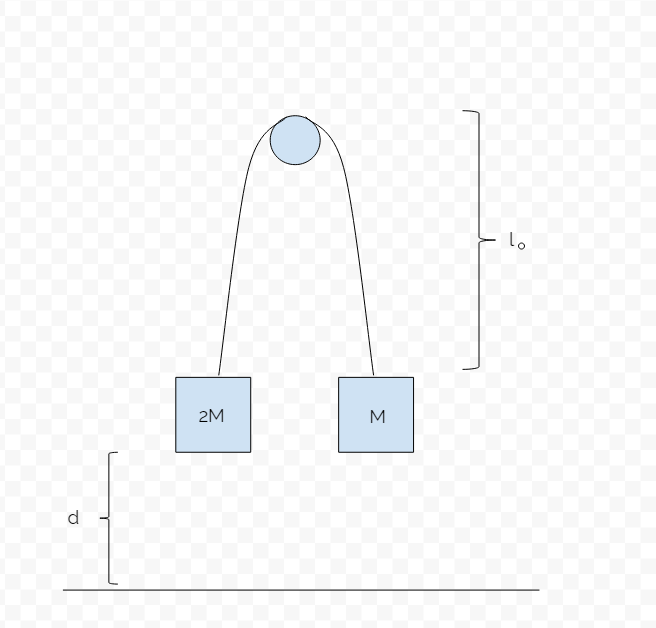
An ideal pulley (massless, frictionless) is set up, as shown in the diagram. Before the system is released, mass M is set into motion as a pendulum. From this initial point in time until the mass 2 M hits the ground, the average period of the oscillation of M is given by
a π ( b ( g l o − d ) + g d c l o sin − 1 l o d ) ,
where a , b , and c are constants. Find a ∗ ( b + c ) .
Note: l o ≥ d .
Temporary Edit: Ignore effects due to centripetal acceleration.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thanks for writing the solution!
I see that the main difference between our methods is that we have found out the average time period differently.
I have used average time period = total time / number of oscillations, I have found out ω a v g = ∫ d t ∫ l g d t and then evaluated T a v g = ω a v g 2 π = ∫ l g d t 2 π ∫ d t .
In your solution, you have found out the instantaneous time period, and then averaged it over the time interval. T a v g = ∫ d t 2 π ∫ g l d t .
Both methods find the average time period per oscillation, but yield different answers. How do we decide which method to use?
We begin with Newton's second law as we find the acceleration of the system. From j ∑ F i j = m a i , we get the system of equations T − M g = M a , and 2 M g − T = 2 M a . Solving for a gives a = g / 3 .
Now we find the time it takes for mass 2 M to hit the ground. Since it's accelerating, we use 2 1 a t 2 = d . Solving for time, and using a = g / 3 , we get a time of t = 6 d / g .
We know that the period of a non-accelerating pendulum is T = 2 π g l . In this problem, l changes with time, and because of the upward acceleration, we replace g with g e f f = g + g / 3 = 4 g / 3 (think equivalence principle).
Now let's find how l changes with time. l decreases in length at the same rate mass 2 M falls, so we can write l t = l o − 6 g t 2 . This means the instantaneous period at time t is T t = 2 π 4 g / 3 l o − 6 g t 2 .
To find the average period from this equation, just integrate T t with respect to time from t = 0 to t = 6 d / g , then divide by the total time.
This comes down to evaluating T a v g = 6 d / g 2 π ∫ 0 6 d / g 4 g / 3 l o − 6 g t 2 d t .
To evaluate, manipulate it to get it in a form of a constant times ∫ 0 x u 2 − t 2 d t = 2 u 2 sin − 1 ( u x ) + x u 2 − x 2 .
This comes out to be, with a great deal of simplifying, 2 π ( g 3 ( l o − d ) + g d 3 l o sin − 1 l o d ) .
Hence, a = 1 / 2 , and b = c = 3 , so a ∗ ( b + c ) = 3 .
Edit: An arithmetical error has been fixed.