Average Speed!
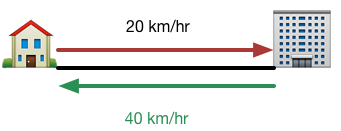
Lokman bikes from her home to her office at a constant speed of 20 km/h, and she bikes back home at a constant speed of 40 km/h. What is closest to the average speed of her bike over time in km/h?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
I don't understand the step from 2S/(S/20+S/40) to 2S/(3S/40) . How did we get to 3S/40 as the divisor?
I intentionally avoided the common misconception, which would be (40+20)/2=30. Instead, I used substitution, so that formulas were not necessary to solve it. Let's say the distance between the office and house is 40 km. Realism aside, this means he would take 2 hours to get to work, and 1 to get back home. So that would be 40km there, 40 back, giving a total of 80km. 80km over a period of 3 hours works out to 26.67 (rounded).
The average speed is the constant speed by which she can travel the same distance at the same time . This mathematically means , The Speed=(Total distance)/(Same period of time), she travel at 20 when she is going , so it takes her T hours . and travel at double the speed when she is going back so that takes her (0.5)T. The common thing is that she travel the same distance . Now back to our first equation , She must travel the same distance and time by this average speed , so Distance traveled = Average speed×Total time. The distance she must travel is double the distance because she goes back and forth and The time must be 1.5 T . So V(1.5T)= 2D , we can rewrite the equation V*1.5T=D+D (remember the two speeds share same distance with different times) therefore V(1.5T)=(20)(T)+40(0.5T) Leading to 1.5VT=20T+20T (cancel T both sides) so 1.5V=40 therefore V=26.666(26.67) (2 d.p)
It's awesome and brilliant answer... Thank you
Let, distance Home to Office =x Then Total distance = Home to Office + Office to Home = 2x
Time for Home to Office t1 = x/20 And, Time for Office to Home t2=x/40 So, Total time t=t1+t2 = (3x)/4
So, Average Speed = (Total distance)/(Total Time) =(2x)*4/(3x) = 26.67
Lokman is a lady?😲
Average speed= 2Rr÷R+r
Where R and r are the constant speeds
Average speed=2(40)(20)÷(40+20)
Average speed =80÷3
Average speed = 26.67 kph
The distance is the same, but if you travel double the speed for the same distance, you'll finish that same distance in half the amount of time. Double the amount of time is spent at going 20 km/h, so I did ( 20 + 20 + 40) / 3 = 26.6 repeating.
Nice! I came with the same solution!
Just want to point out that the actual is 0 km/h, considering there was no displacement :)
That is the average velocity I think - displacement/time. As there was no displacement the average velocity would be 0 km/h. Average speed is the distance traveled over time - so in this case since there was distance traveled (there and back) there is an average speed. Speed and velocity are different in this way (and would be the same if the displacement is the same as distance traveled - this could be the case if the direction wasn't changed). Correct me if I'm mistaken...
Because she's going half-speed, her morning commute takes twice as long. Therefore, in her first duration-of-her-ride-home, she goes 20 kph, in her second duration-of-her-ride-home, she's still going 20 kph, and in her third (and final) duration-of-her-ride-home, she's going 40 kph. Therefore her average speed is the average of {20, 20, & 40} kph, 26.7 kph.
(The temptation to average 20 and 40 is weighting the trips by distance instead of time. But average speed is total distance over total time; this quantity's average must therefore be time-weighted. (If unconvinced, compute the total distance and total time and see what the resultant speed corresponds to, and try and track why.))
according to To-ong's theorem, speed can be related to as a harmony, thus this problem can be related to harmonic mean 2ab/a + b 2(40)(20)/40+20 = 26.667
To everyone doing the algebra. I believe that the algebra is not a real life solution. The mean average provides an answer of 30. This is the reality. I love my algebra but I do not believe it gives an accurate answer on this occasion. Sorry. You have my permission to reply, in capitals if warranted. :)
Log in to reply
Sr you, but in real life people have to do this algebra in the same way , this answer just only one 26,67 - For me, this datas, mentioned in this quizz, it maybe impossible in real life :) - however, if you plus two speed then divided to 2, it is a big problem, because her speed in the street from office to home, which is greater than the first 2 times , you can only do the equation that is, when she moves in the same speed on 1 street, then the way she go home and office all in the same time :)

It's a very common mistake done by people when dealing with average speed. The mathematical average of the initial and final speed, in this case 2 2 0 + 4 0 = 3 0 is called the mean speed and is not always the same as average speed. They become same if the acceleration is constant.
The average speed is defined as, Total time taken Total distance traveled .
For this problem, let's assume the distance from home to office is ′ s k m ′ and time taken to go and come from office are ′ t 1 ′ & ′ t 2 ′ hours respectively. Then, Average speed = t 1 + t 2 2 s = 2 0 s + 4 0 s 2 s [ As, Time = Speed Distance ] = 4 0 3 s 2 s = 3 2 × 4 0 ≈ 2 6 . 6 7