Avoiding in a circle

Classical Mechanics Level 3

An ambulance car is going with a speed of 60 km/h 60~\mbox{km/h} , while a car is trying to go around it in a circle with a speed 50 km/h 50~\mbox{km/h} . If the sound that ambulance car emits has a frequency of 1 kHz 1~\mbox{kHz} , which frequency does the driver of the car hear in Hz when the ambulance car is in the center of the circle it makes, and the car makes an angle θ = 3 0 ∘ \theta = 30^\circ with the direction of the car?

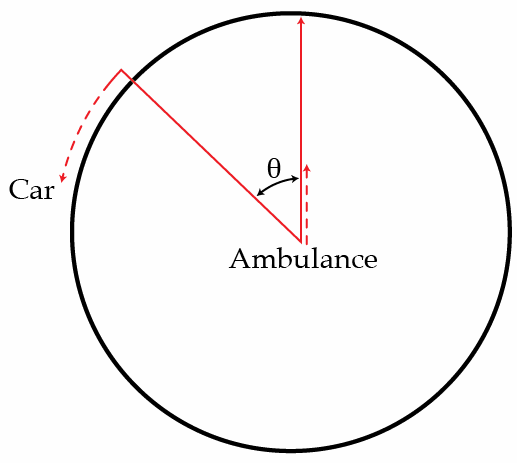
Details and assumptions

  • Speed of sound in the air is c = 1235 km/h c = 1235~\mbox{km/h} .


The answer is 1044.

View wiki
David Mattingly by David Mattingly

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Yuchen Liu
Sep 16, 2013

The ambulance moves upwards at 60 k m / h 60km/h

When it is at the centre of the circle, resolving the components of its velocity, the ambulance is moving at 30 3 k m / h 30\sqrt3km/h towards the car. Whereas the car moves perpendicular to that direction.

Hence the frequency heard by the listener is

f = f 0 v s o u n d v s o u n d − v s o u r c e = 1000 ∗ 1235 1235 − 30 3 = 1044 f=f_0 \frac{v_{sound}}{v_{sound}-v_{source}}=1000*\frac{1235}{1235-30\sqrt3}=\boxed{1044}

15 Helpful 0 Interesting 1 Brilliant 2 Confused

Did you use:

(freq. to the car) = (freq. of the source)* [(V.sound + V.car) / (V.sound + V.source)]

Velocity of the car and source in reference to an axis linking the two. Hence V.car = 50 cos(90º) and V.source = -60 cos(60º). V.source is negative because it's approaching the car.

Pedro Vieira - 7 years, 8 months ago
Andrew Song
Aug 18, 2015

If the ambulance were to remain in place, the observed frequency would equal the siren's frequency. However, when the ambulance moves north, only the cosine component of ambulance's velocity is considered; it would be v a m b c o s θ v_{amb} cos \theta towards the car. Hence, f o b s = f c c − v a m b c o s θ f_{obs} = f \frac{c}{c-v_{amb} cos \theta} .

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Gopal Bhakat
Sep 16, 2013

Here the effective speed of sound at the direction of the car is its original sound plus the cos component of the speed of ambulance. The speed of the car would not play any role as the direction of the car and the direction of the sound reaching the car are at perpendicular. So the effective speed of sound is calculated as 1235+60 cos(60)=1286 km/hr. Now the no of sound wave reaching the car is proportional to the effective speed of the sound. So the ans is 1000 1286/1235=1042.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

It is cos(30)

Vedant Parwal - 4 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...