4 Circles in Love
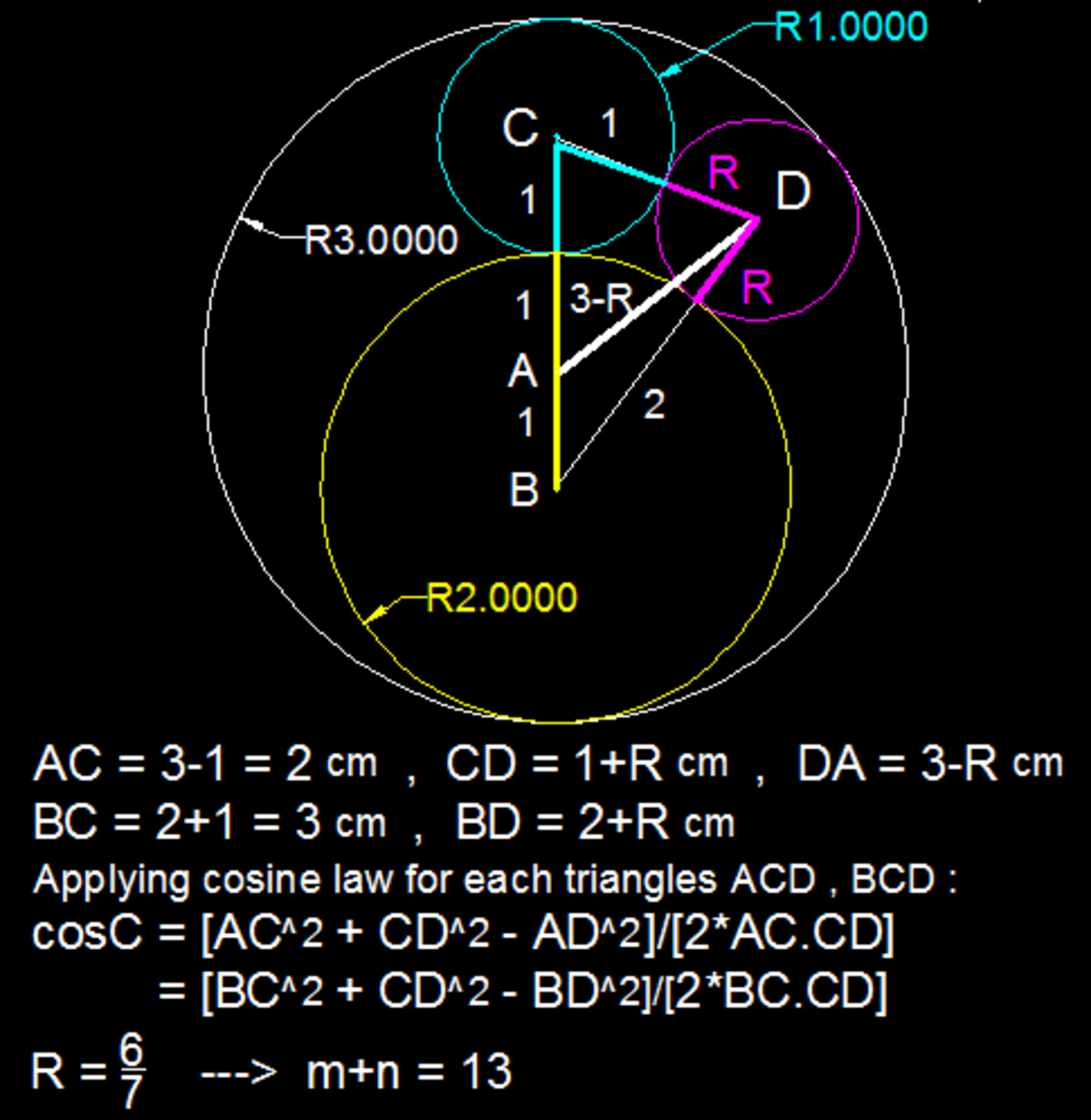
The diagram above shows 4 mutually tangent circles.
Their respective radii (in centimeters) in descending order of magnitude are 3, 2, 1, and n m , where m and n are coprime positive integers. What is m + n ?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I think it's worth the time to explain why some curvatures k i 's are positive while some is/are negative.
Can you elaborate on that?
Stewart's Theorem will work also.
Exactly what I did!
In general, if three circles of radii a, b & c are touching each other externally then the radius ( R ) of circle which touch all three circles internally, is given by a general formula (for detailed analysis of three tangent circles go through: Geometry of three externally touching circles by H.C. Rajpoot )
\boxed{\color{dark black}{R=\frac{abc}{2\sqrt{abc(a+b+c)}-ab-bc-ca}}\quad \underbrace{\{\forall \ 0<c\le a, b<R \quad \text{\&}\quad c>\frac{ab}{(\sqrt a+\sqrt b)^2}}_{\text{conditions for validity of formula}\}}}
As per given problem, the given values of radii are R = 3 , a = 1 , b = 2 , c = ? , substituting these values in above general formula
3 = 2 1 ⋅ 2 ⋅ c ( 1 + 2 + c ) − 1 ⋅ 2 − 2 ⋅ c − c ⋅ 2 1 ⋅ 2 ⋅ c
6 2 c 2 + 6 c = 1 1 c + 6
( 6 2 c 2 + 6 c ) 2 = ( 1 1 c + 6 ) 2
4 9 c 2 − 8 4 c + 3 6 = 0
c = 2 ( 4 9 ) − ( − 8 4 ) ± ( − 8 4 ) 2 − 4 ( 3 6 ) ( 4 9 ) = 9 8 8 4 = 7 6 = n m
∴ m + n = 6 + 7 = 1 3
We can try Descartes' kissing circles.
Can you elaborate?
It was already explained by Niranjan Khanderia sir.
Relevant wiki: Descartes' Circle Theorem
Let r > 0 denote the radius that we're looking for, then using the statement given in the aforementioned theorem:
The curvatures of all these inner circles are the positive reciprocal of their respective radius, whereas the curvature of the external circle has a negative curvature.
Thus, k 1 = r , k 2 = 2 1 , k 3 = 2 1 , k 4 = − 3 1 .
And the theorem states that
( k 1 + k 2 + k 3 + k 4 ) 2 = 2 ( k 1 2 + k 2 2 + k 3 2 + k 4 2 )
Plugging in these values and simplify gives
( 6 7 − r ) 2 = 2 ( 3 6 4 9 + r 2 )
so solving for r gives r = n m = 6 7 . The answer is m + n = 1 3 .