Awesome geometry - 9
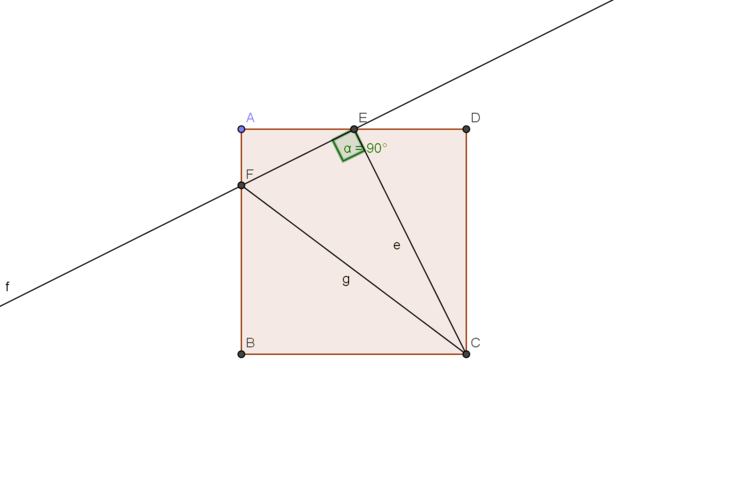 In square ABCD ,
In square ABCD ,
Point E is the mid point of AD.
Join CE.
Let Point F be on AB such that angle CEF measures 90 .
If measure of angle CED is 63.43 ,
Find the measure of angle ECF. Give your answer to correct 2 decimals.
This problem is a part of set Awesome ' NIHARIAN' geometry
The answer is 26.57.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Well Done Sir!
It is easy to realize that two triangles CEF and CED are uniform. So: ∠ C E D = ∠ E F C ⇒ ∠ E C F = 9 0 0 − ∠ E F C = 2 6 . 5 7
We know that ∠ C D E = ∠ E A F = 9 0 ∘ and also ∠ D E C + ∠ A E F = ∠ D E C + ∠ E C D = 1 8 0 − 9 0 = 9 0 ∘
⟹ ∠ A E F = ∠ E C D ⟹ △ A E F ∼ △ D E C (AA)
⟹ ∠ E F A = ∠ D E C = 6 3 . 4 3 ∘
Now, prolong C D until it meets f at H
We have ∠ A E F = ∠ H E D , ∠ E A F = ∠ E D H = 9 0 ∘ and, since E is the midpoint of A D , A E = E D ⟹ △ A E F ≅ △ H E D (ASA)
Now it gets interesting: from the congruence between △ A E F and △ H E D and from the fact that ∠ C E F = 9 0 ∘ , we can say that E C is both a median and a height of △ F C H , which means that △ F C H is isosceles, with ∠ C F E = ∠ C H E = ∠ E F A = ∠ D E C = 6 3 . 4 3 ∘ , and that E C is also the bisector of ∠ H C F
⟹ ∠ E C F = 2 ∠ H C F = 2 1 8 0 − 2 × 6 3 . 4 3 = 2 6 . 5 7 ∘
tan C E D = S / ( S / 2 ) = 2 ⟹ C E D = a r c t a n ( 2 ) = 6 3 . 4 3 .
I n △ E F A , ∠ E F A = 9 0 − ∠ F E A = c o m p l i m e n t a r y a n g l e ∠ C E D . ⟹ t w o a n g l e s o f r i g h t a n g l e d △ s E F A a n d C E D a r e e q u a l . ∴ △ s E F A a n d C E D a r e S I M I L A R . ∴ i n △ s E F A a n d C E D , h y p o t e n u s e C E h y p o t e n u s e F E = C D E A = S S / 2 = 1 / 2 = tan ( 2 6 . 5 7 ) . B u t i n △ F C E , ∠ E C F = t a n − 1 ( C E F E ) = t a n − 1 ( 1 / 2 ) = 2 6 . 5 7
Sorry I have made changes, it was to make it better.